Слободянюк А.И. Физика 10/13.5

Содержание книги

Предыдующая страница

§13. Взаимодействие магнитного поля с веществом

13.5 Взаимодействие постоянных магнитов.

Знание формы и намагниченности постоянного магнита позволяет для расчетов заменить его эквивалентной системой электрических токов намагничивания. Такая замена возможна как при расчете характеристик магнитного поля, так и при расчетах сил, действующих на магнит со стороны внешнего поля.

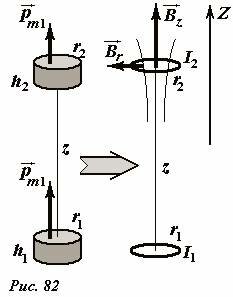
Для примера проведем расчет силы взаимодействия двух постоянных магнитов. Пусть магниты имеют форму тонкого цилиндра, их радиусы обозначим r₁ и r₂, толщины h₁, h₂ , оси магнитов совпадают, расстояние между магнитами обозначим z, будем считать, что оно значительно больше размеров магнитов (Рис. 82).

Возникновение силы взаимодействия между магнитами объясняется традиционным способом: один магнит создает магнитное поле, которое воздействует на второй магнит. Для расчета силы взаимодействия мысленно заменим магниты с однородной намагниченностью J₁ и J₂ круговыми токами, текущими по боковой поверхности цилиндров. Силы этих токов выразим через намагниченности магнитов

\(~I_{1,2} = J_{1,2} h_{1,2}\) , (1)

а их радиусы будем считать равными радиусам магнитов. Разложим вектор индукции \(~\vec B\) магнитного поля, создаваемого первым магнитом в месте расположения второго на две составляющие: осевую \(~\vec B_z\) , направленную вдоль оси магнита, и радиальную \(~\vec B_r\) - перпендикулярную ей. Для вычисления суммарной силы, действующей на кольцо, необходимо мысленно разбить его на малые элементы IΔl и просуммировать силы Ампера, действующие на каждые такой элемент. Используя правило левой руки, легко показать, что осевая составляющая магнитного поля приводит к появлению сил Ампера, стремящихся растянуть (или сжать) кольцо – векторная сумма этих сил равна нулю. Наличие радиальной составляющей поля приводит к возникновению сил Ампера, направленных вдоль оси магнитов, то есть к их притяжению или отталкиванию.

Задание для самостоятельной работы.

1. Убедитесь, что магниты притягиваются, если электрические токи текут в одном направлении, и отталкиваются, если токи текут в противоположных направлениях. Свяжите направления токов намагничивания с полюсами магнитов (северным и южным) и убедитесь, что разноименные полюса притягиваются, а одноименные отталкиваются.

Так как рассматриваемая система обладает осевой симметрией, то модуль радиальной составляющей постоянен во всех точках кольцевого тока второго магнита. Следовательно, проекция силы, действующей на второй магнит, с учетом правила левой руки, определяется формулой

\(~F = -I_2 B_r l = -I_2 B_r 2 \pi r_2\) . (2)

Положительное направление силы соответствует притяжению магнитов, положительное направление тока традиционно – против часовой стрелки.

Магнитное поле, создаваемое первым магнитом, эквивалентно полю кругового тока (см. §12.7.1). В рамках сделанных приближений (z >> r,h), осевая составляющая поля определяется формулой

\(~B_z = \frac{\mu_0 p_{m1}}{2 \pi z^3}\) , (3)

где \(p_{m1} = I_1 S_1 = J_1 h_1 \pi r^2_1 = J_1 V_1\) - магнитный момент первого магнита (V₁ - его объем).

Радиальную составляющую поля мы нашли с помощью о магнитном потоке, в месте расположения второго кругового контура она равна (см. §12.12)

\(~B_r = -\frac{r_2}{2} \cdot \frac{\Delta B_z}{\Delta z} = \frac{3 \mu_0 p_{m1}}{4 \pi z^4} r_2\) . (4)

Уменьшение осевой составляющей поля приводит к появлению положительной (направленной от оси) составляющей поля.

Важно подчеркнуть, что сила взаимодействия между магнитами определяется скоростью изменения осевой составляющей поля \(~\frac{\Delta B_z}{\Delta z}\), если бы поле, создаваемое первым магнитом было однородным, то сила, действующая на второй магнит, была бы равна нулю.

Этот вывод можно обобщить на случай произвольного контура с током (следовательно, и на любой постоянный магнит). Действительно, сила Ампера, действующая на элемент тока \(~I \Delta \vec l_k\) равна \(~\Delta \vec F_k = I \Delta \vec l_k \times \vec B\), для вычисления силы, действующей на контур необходимо просуммировать эти выражения по всем элементам контура

\(~\vec F = \sum_k \Delta \vec F_k = \sum_k I \Delta \vec l_k \times \vec B = I (\sum_k \Delta \vec l_k) \times \vec B = \vec 0\)

При выводе учтено, что в однородном поле вектор индукции постоянен, поэтому его можно вынести за знак суммы, а сумма элементов контура равна нулю, так как все эти векторы выстроены в замкнутую линию – конец последнего совпадает с началом первого. Следовательно, сила действующая на любой постоянный магнит, находящийся во внешнем однородном поле равна нулю. Аналогично, сила, действующая на электрический диполь со стороны однородного электрического поля также равна нулю, а в неоднородном поле эта сила пропорциональна скорости изменения поля \(~\frac{\Delta E}{\Delta z}\).

Подставляя выражение для радиальной составляющей поля, получим формулу, для вычисления силы взаимодействия двух магнитов в рассматриваемом случае

\(~F = -I_2 \cdot 2 \pi r_2 \cdot B_r = -I_2 \cdot 2 \pi r_2 \cdot \frac{3 \mu_0 p_{m1}}{4 \pi z^4} r_2 = I_2 \cdot \pi r^2_2 \cdot \frac{3 \mu_0 p_{m1}}{2 \pi z^4} = \frac{3 \mu_0 p_{m1} p_{m2}}{2 \pi z^4}\) . (5)

где \(p_{m2} = I_2 S_2 = J_2 h_2 \pi r^2_2 = J_2 V_2\) - магнитный момент второго магнита. Так, например для двух одинаковых магнитов с размерами h = r = 1 см с намагниченностью J ≈ 4·10⁵ А , находящихся на расстоянии z = 5 см сила взаимодействия приблизительно равна 0,15 Н.

Обратим внимание, что в формулу (5) в качестве характеристик магнитов входят только их магнитные моменты, поэтому эта формула может применяться для магнитов любой формы, важно только чтобы расстояние между ними превышало их размеры, и их магнитные моменты были параллельны. Также следует заметить, что сила взаимодействия между магнитами обратно пропорциональна четвертой степени расстояния между ними, что является следствием диполь-дипольного характера взаимодействия (для несуществующих точечных магнитных зарядов эта сила была бы, как обычно, обратно пропорциональна квадрату расстояния).

Примечания

Следующая страница