Слободянюк А.И. Физика 10/15.1.II
§15. Переменное электромагнитное поле
15.1 Явление электромагнитной индукции.
15.1.3 «Движущееся» магнитное поле вблизи проводника.
Рассмотрим теперь процессы, проходящие в проводнике, относительно которого движется источник магнитного поля. Причем не существенно, что представляет собой этот источник, им может быть как постоянный магнит, так и проводники с постоянным током. Пусть для определенности цилиндрический постоянный магнит движется относительно неподвижного проводящего кругового контура L. Результаты экспериментов М. Фарадея и его многочисленных последователей однозначно свидетельствуют, что в контуре возникает электрический ток, точно такой же, как и в случае движения контура. Иными словами, индукционный ток полностью определяется относительным движение контура и магнита, и никакими измерениями и исследованиями нельзя различить, что движется проводник или магнит.
Эти и подобные эксперименты во многом способствовали тому, что принцип относительности Г. Галилея в механике был распространен сначала на электромагнитные, а затем и на все физические явления. В настоящее время принцип относительности является одним из фундаментальных физических принципов, справедливость которого подтверждена и постоянно подтверждается всем развитием естественных наук. Итак, если мы принимаем за физическую аксиому[1] принцип относительности: никакие физические эксперименты не позволяют отличить состояние покоя от состояния равномерного и прямолинейного движения, или равносильно: все физические явления протекают одинаково во всех инерциальных системах отсчета.
На этом можно и закончить изложение материала данного раздела, для чего следует перейти в систему отсчета, связанную с магнитом, и рассмотреть движение проводника в магнитном поле, что уже сделано ранее. Тем не менее, имеет смысл дать физическую трактовку возникновения электрического тока в неподвижном проводнике, относительно которого движется магнит. В случае неподвижного проводника средняя скорость движения свободных заряженных частиц равна нулю, поэтому и среднее значение силы Лоренца также равно нулю. Но если в проводящем контуре, обладающем электрическим сопротивлением, существует электрический ток, то в контуре должны действовать сторонние силы! Следовательно, мы должны указать силы, действующие на свободные заряды и приводящие их в движение. Как было сказано, характеристики индукционного электрического тока в проводнике не зависят от того, движется проводник или магнит, результат действия поля на проводник не должен зависеть от выбранной системы отсчета, в которой проводится описание. Так, например, если проводник нагрелся, то повышение его температуры одинаково во всех системах отсчета, если проводник расплавился или разорвался под действием поля, то с ним это произошло в любой системе отсчета. Более простой пример: сила, действующая на проводник со стороны поля должна быть одинакова во всех инерциальных системах отсчета, наконец, сила, действующая на свободные заряды также должна быть одинакова во всех системах отсчета.
В системе отсчета, связанной с магнитом (когда движется проводник), такой силой является сила Лоренца. В системе отсчета связанной с проводником (где он покоится) на заряженные частицы должна действовать такая же сила. Сила Лоренца пропорциональна заряду частицы, сам же заряд является инвариантной физической величиной, не зависящей от системы отсчета. Следовательно, в системе отсчета, связанной с проводником, на заряженные частицы действует сила, пропорциональная заряду частицы. Сила, пропорциональная заряду, есть сила, действующая со стороны электрического поля.
По-видимому, можно было придумать какое другое название этой силе, но если эта сила пропорциональна электрическому заряду частицы, то нет даже принципиальной возможности отличить эту силу от силы, действующей со стороны электрического поля. Характеристикой этой силы также может служить отношение силы к величине заряда, то есть напряженность электрического поля. Так стоит ли «придумывать» новые силы, новые явления, если все развитие физики идет по пути обобщения, сведения многочисленных явлений ко все меньшему количеству единых фундаментальных взаимодействий. Наконец, самое существенное: электрическое поле, которое создается движущимся магнитом, обладает теми же свойствами, что и «обычное» электрическое поле, создаваемое электрическими зарядами – оно воздействует на другие заряды, и как мы покажем в дальнейшем, оно способно порождать магнитное поле.
Таким образом, мы должны признать, что в системе отсчета, в которой постоянный магнит движется, помимо магнитного поля должно существовать электрическое поле. Или: движущийся магнит создает электрическое поле.
По существу мы об этом уже говорили, когда рассматривали источники магнитного поля. Источниками магнитного поля являются движущиеся электрические заряды, но движущиеся относительно чего? Аналогичная ситуация рассматривается сейчас: движущийся магнит создает электрическое поле, движущийся относительно чего? Если механическое движение относительно, то относительно и электромагнитное поле. То есть реальность является единое электромагнитное поле, которое в некоторых случаях, в некоторых системах отсчета можно описывать как электростатическое; в некоторых случаях, в некоторых системах отсчета как магнитостатическое. Ответ на вопрос о разделении поля на электрическое и магнитное зависит от выбора системы отсчета, в которой проводится описание.
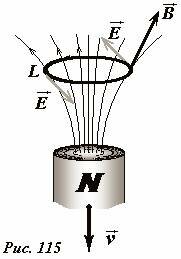
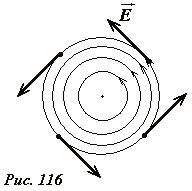
Вернемся в систему отсчета, в которой проводник покоится, но в нем возникает электрический ток. Мы пришли к выводу, что в качестве сторонних сил в данном случае выступают силы со стороны электрического поля. Причем работа этих сил по замкнутому контуру не равна нулю. Следовательно, это электрическое поле не является потенциальным, в этом его главное отличие от электростатического поля, создаваемого неподвижными зарядами. В рассматриваемом примере (Рис. 115) во всех точках проводящего контура электрическая сила направлена по касательной к контуру, следовательно, силовая линия этого поля является окружностью, то есть замкнутой кривой. Структура силовых линий такого поля совпадает со структурой линий магнитного поля прямого тока – набор концентрических окружностей (Рис. 116). Конечно, в данном случае такая структура силовых линий однозначно связана с осевой симметрией его источника (магнита, вектор скорости которого направлен вдоль оси). В общем случае силовые линии этого поля отличаются от окружности, но являются замкнутыми, образуя набор «вихрей». Поэтому данное электрическое поле называется вихревым.
Так как магнит в целом электрически нейтрален (его суммарный заряд равен нулю), то поток вектора напряженности рассматриваемого электрического поля через любую замкнутую поверхность равен нулю, поэтому можно вспомнить все наши рассуждения по поводу доказательства замкнутости магнитных силовых линий и повторить их здесь для вихревого электрического поля.
Возникновение вихревого электрического поля при движении магнита не зависит от того, находится ли в этом поле проводник. Рассматриваемый нами проводящий контур выступает в роли прибора, позволяющего зафиксировать существование электрического поля. Поэтому разумно, вместо характеристик электрического тока в реальном кольце, рассматривать характеристики индуцированного вихревого электрического поля. Мы установили формулу для ЭДС индукции, возникающей в контуре
где Φ(t) - изменяющийся магнитный поток через контур. Эту же величина равна работе, которую совершает вихревое электрическое поле по перемещению единичного положительного заряда, в данном осесимметричном случае – произведению напряженности электрического поля E на длину контура
приравнивая эти выражения, получим значение модуля напряженности поля
Как было показано ранее, формула (1) для ЭДС индукции в контуре справедлива для произвольного магнитного поля и произвольного контура.
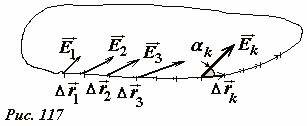
Выразим ЭДС индукции, возникающей в контуре через напряженность электрического поля. Для этого мысленно разобьем контур на малые участки, каждый из которых задается малым вектором \(~\Delta \vec r_k\) (k = 1,2,3...), на каждом участке найдем вектор напряженности поля \(~\vec E_k\), образующим угол αk с вектором \(~\Delta \vec r_k\) (Рис. 117). Тогда работа по перемещению единичного заряда по контуру (то есть ЭДС) выразится суммой
которая представляет собой ни что иное, как циркуляцию вектора напряженности электрического поля ГE. Таким образом, закон электромагнитной индукции можно выразить через характеристики полей, исключив реальный проводящий контур:
Циркуляция вектора напряженности электрического поля по любому контуру равна скорости изменения магнитного потока через этот контур, взятой с противоположным знаком
Если под действием поля движущегося магнита в контуре возникает электрический ток, то этот ток может совершать работу (в простейшем случае – в контуре будет выделяться теплота), следовательно, он обладает энергией. Эта энергия не может появиться сама по себе – закон сохранения энергии незыблем и в этом случае. Дело в том, что индуцированный ток создает магнитное поле, которое воздействует на движущийся магнит. Поэтому, если мы хотим, чтобы скорость движения магнита не изменялась, то к нему нужно прикладывать внешнюю силу. Работа этой силы в точности равна энергии индуцированного тока.
15.1.4. Изменяющееся магнитное поле.
Обсудим, наконец, последнюю группу экспериментов, связанных с «превращением магнетизма в электричество». В замкнутом проводнике, помещенном в переменное магнитное поле, также возникает электрический ток. Это явление может быть сведено к рассмотренным выше, если стать на точку зрения теории близкодействия. Напомним, в применении к электромагнитным явлениям эта теория утверждает, что переносчиком взаимодействий является реально существующее электромагнитное поле, как объективная реальность, как вид материи. Два электрически заряженных тела непосредственно не взаимодействую между собой: один заряд (как источник) создает электромагнитное поле, которое воздействует на другой заряд (который выступает в роли прибора, регистрирующего наличие поля). То есть второй заряд-приемник «чувствует»,воспринимает то поле, которое существует в той малой области пространства, где он непосредственно находится. Изменение положения или величины заряда-источника приведет к изменению силы, действующей на приемник не мгновенно, а через некоторый промежуток времени, который потребуется, чтобы изменение (возмущение) поля распространилось от одного заряда к другому. Аналогичные рассуждения можно провести и для магнитных взаимодействий. Иными словами любой прибор, регистрирующий характеристики электромагнитного поля воспринимает поле только в той области, где он находится. Причина этого заключается не в недостатках, несовершенстве приборов, а в самих свойствах электромагнитного поля - нет принципиальной возможности однозначно определить характеристики источников поля по изучению параметров поля в ограниченной области пространства в ограниченный промежуток времени. Простейший пример: в «черном ящике» находится источник магнитного поля. Изучая характеристики поля вне ящика, мы никакими методами не можем сказать, что находится в ящике – постоянный магнит, или катушка, по которой протекает электрический ток.
Поэтическим выражением этого положения является известная строка «...как свет угасших звезд доходит». Наблюдая (исследуя любыми самыми совершенными приборами) свет далекой звезды (то есть электромагнитное поле, испущенное много лет назад) мы не можем сказать, где эта звезда находится «сейчас», существует ли она «сейчас»[2].
Обобщая данные рассуждения, можно сформулировать один из основных принципов теории электромагнитного поля: свойства электромагнитных полей проявляются локально, например, изменяющееся в данной точке[3] магнитное поле приводит к возникновению электрического поля в этой же точке.
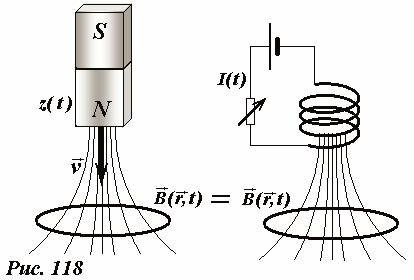
Рассмотрим еще раз металлическое кольцо, относительно которого движется постоянный магнит (Рис. 118). ЭДС индукции и ее последствия (электрический ток, нагрев проводника и т.д.) определяются вектором индукции поля в точках кольца и его зависимостью от времени \(~\vec B(\vec r,t)\). Пространственная структура магнитного поля зависят от свойств постоянного магнита (его формой, размерами, намагниченностью). Зависимость этого поля от времени в точках кольца определяется изменением положения магнита - его координатой как функцией времени z(t). Пусть теперь магнитное поле создается электрическим током в неподвижной катушке. В принципе возможно (законы физики этого не запрещают) создать такую катушку и так изменять силу тока в ней I(t), чтобы во всех точках кольца магнитное поля изменялось так же, как и магнитное поле, созданное движущимся постоянным магнитом. Будут ли в этих двух различных случаях отличаться характеристики ЭДС и электрического тока в кольце? С точки зрения теории близкодействия – нет! Кольцо и содержащиеся в нем заряженные частицы «не могут знать» почему изменяется действующее на них электромагнитное поле: или из-за движения магнита, или из-за изменения силы в неподвижной катушке.
Таким образом, мы обязаны сделать вывод – изменяющееся магнитное поле создает вихревое электрическое поле, не зависимо от причины, вызывающей изменение магнитного поля. Причем характеристики вихревого электрического поля однозначно определяются законом изменения магнитного поля. Следовательно, и в этом случае остается справедливой прежняя формулировка закона электромагнитной индукции – ЭДС индукции в контуре равна скорости изменения магнитного потока через контур.
С энергетической точки зрения и в этом случае все обстоит «благополучно»: возникающий в контуре электрический ток создает магнитное поле, индуцирующее в первичной цепи ЭДС, направленную против ЭДС источника, заставляя тем самым его совершать большую работу. Строгий расчет показывает, что эта дополнительная работа в точности равна энергии индуцированного тока.
15.1.5. Закон электромагнитной индукции Фарадея.
Мы достаточно подробно рассмотрели три различных, на первый взгляд, варианта явления электромагнитной индукции, возникновения электрического тока в проводящем контуре под действием магнитного поля: при движении проводника в постоянном магнитном поле; при движении источника магнитного поля; при изменении во времени магнитного поля. Во всех этих случаях закон электромагнитной индукции одинаков:
ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через контур, взятой с противоположным знаком
независимо от причин, приводящих к изменению этого потока.
Уточним некоторые детали приведенной формулировки.
Первое. Магнитный поток через контур может изменяться произвольным образом, то есть функция Φ(t) не обязана всегда быть линейной, а может быть любой. Если магнитный поток изменяется по линейному закону, то ЭДС индукции в контуре постоянна, в этом случае величина интервала времени Δt может быть произвольной, значение отношения (1) в этом случае не зависит от величины этого интервала. Если же поток изменяется более сложным образом, то величина ЭДС не является постоянной, а зависит от времени. В этом случае рассматриваемый интервал времени следует считать бесконечно малым, тогда отношение (1) с математической точки зрения превращается в производную от функции магнитного потока по времени. Математически этот переход полностью аналогичен переходу от средней к мгновенной скорости в кинематике.
Второе. Понятие потока векторного поля применимо только к поверхности, поэтому необходимо уточнять о какой поверхности идет речь в формулировке закона. Однако, поток магнитного поля через любую замкнутую поверхность равен нулю. Поэтому для двух различных поверхностей, опирающихся на контур магнитные потоки одинаковы. Представьте себе поток жидкости, вытекающий из отверстия. Какую бы вы не выбрали поверхность, границей которого являются границы отверстия, потоки через них будут одинаковы. Здесь уместна еще одна аналогия: если работа силы по замкнутому контуру равна нулю, то работа этой силы не зависит от формы траектории, а определяется только ее начальной и конечной точками.
Третье. Знак минус в формулировке закона имеет глубокий физический смысл, фактически он обеспечивает выполнение закона сохранения энергии в этих явлениях. Этот знак является выражением правила Ленца. Пожалуй, это единственный случай в физике, когда один знак удостоился собственного имени.
Как мы показали, во всех случаях физическая сущность явления электромагнитной индукции одинакова и кратко формулируется следующим образом: переменное магнитное поле порождает вихревое электрическое поле. С этой, полевой, точки зрения закон электромагнитной индукции выражается через характеристики электромагнитного поля: циркуляция вектора напряженности электрического поля по любому контуру равна скорости изменения магнитного потока через этот контур
В этой трактовке явления существенно, что вихревое электрическое поле возникает при изменении магнитного поля, независимо от того, имеется ли реальный замкнутый проводник (контур), в котором возникает ток или нет. Это реальный контур может играть роль прибора, для обнаружения индуцированного поля.
Наконец, еще раз подчеркнем – электрические и магнитные поля относительны, то есть их характеристики зависят выбора системы отсчета, в которой дается их описание. Однако, этот произвол в выборе системы отсчета, в выборе способа описания не приводит к каким-либо противоречиям. Измеряемые физические величины инвариантны, не зависят от выбора системы отсчета. Например, сила, действующая на заряженное тело со стороны электромагнитного поля, не зависит от выбора системы отсчета. Но при ее описании в одних системах она может трактоваться как сила Лоренца, в других к ней может «добавляться» электрическая сила. Аналогично (даже как следствие) ЭДС индукции в контуре (сила индуцированного тока, количество выделившейся теплоты, возможная деформация контура и т.д.) не зависят от выбора системы отсчета.
Как всегда предоставляемой свободой выбора можно и необходимо пользоваться – всегда есть возможность выбрать тот метод описания, который вам больше нравится – как наиболее простой, наиболее наглядный, наиболее привычный и т.д.
15.1.6. Явление самоиндукции. Индуктивность.
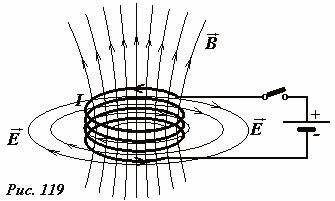
Как было показано ранее, любое переменное магнитное создает вихревое электрическое поле. Если в некоторой цепи (Рис. 119) изменяется электрический ток, то этот ток создает изменяющееся магнитное поле \(~\vec B\), которое приводит к появлению вихревого электрического поля \(~\vec E\). Причем это поле появляется во всех точках пространства, где изменяется поле магнитное, в том числе и проводниках, образующих электрическую цепь. Таким образом, изменяющийся ток посредством переменного магнитного поля оказывает воздействие на себя самого. Явление возникновения ЭДС в цепи вследствие изменения силы тока в этой же цепи называется самоиндукцией. Это явление является частным случаем электромагнитной индукции, поэтому формула для ЭДС самоиндукции εsi остается прежней
где Φ - магнитный поток поля, создаваемого током в контуре. В соответствии с правилом Ленца возможный индукционный ток препятствует изменению магнитного потока через контур. Поэтому ЭДС самоиндукции препятствует изменению тока в цепи. Так если ток в цепи возрастает, то возрастает и магнитный поток, поэтому направление индукционного тока противоположно исходному току. При уменьшении силы тока в цепи, ЭДС индукции поддерживает затухающий ток.
Задание для самостоятельной работы.
- Используя правила для определения направления индукции поля и направления индуцированного электрического поля, определите направления векторов этих полей в случаях включения и выключения тока в схеме на рис. 119.
Фигурирующий в формуле (1) магнитный поток всегда пропорционален силе тока в цепи I , так он является потоком поля, созданного этим током
коэффициент пропорциональности в этом выражении называется индуктивностью цепи.
Используя это выражение для магнитного потока и закон электромагнитной индукции легко получить формулу для ЭДС самоиндукции, возникающей в цепи при изменении электрического тока
Величина индуктивности полностью определяется геометрическими размерами и формой цепи и магнитными свойствами среды, в которой расположена цепь. Часто индуктивность относят не ко всей цепи, а к некоторым ее элементам. Следует подчеркнуть, что любая электрическая цепь, любой ее элемент обладает индуктивностью. Однако во многих случаях явление самоиндукции оказывает настолько слабое влияние на ток в цепи, что часто им пренебрегают. Понятно, что это явление полностью отсутствует в цепях постоянного тока, когда токи и созданные ими магнитные поля не изменяются. В таких цепях явления самоиндукции могут играть заметную роль только в моменты включения и выключения тока, когда поля могут изменяться достаточно резко и приводить к появлению сильных индукционных токов.
Индуктивность является важной характеристикой элементов цепи, поэтому в Международной системе единиц СИ введена специальная единица измерения Генри (сокращенно Гн), названная в честь американского физика Джозефа Генри (1797 – 1878). Индуктивностью в 1 Генри обладает электрическая цепь (или элемент цепи), в которой при изменении тока на 1 Ампер за 1 секунду возникает ЭДС самоиндукции, равная 1 Вольту.
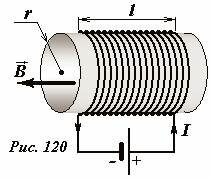
Наибольшей индуктивностью обладают катушки (соленоиды) с большим числом витков. В такой катушке ЭДС индукции возникает в каждом витке, поэтому ее суммарное значение может быть очень заметным. Рассчитаем индуктивность длинной цилиндрической катушки (соленоида) длиной l, содержащей N проволочных витков, плотно намотанных на сердечник радиуса r, изготовленный из материала с магнитной проницаемостью μ (Рис. 120). Если по обмотке соленоида протекает электрический ток силой I, то внутри его создается магнитное поле индуктивности \(~\vec B\), направленное вдоль оси, причем модуль этого вектора равен
где \(~n = \frac{N}{l}\) - плотность намотки, т.е. число витков на единицу длины.
Так как магнитное поле внутри соленоида однородное (если пренебречь краевыми эффектами), то магнитный поток через один виток равен \(\Phi_1 = BS\) (\(S = \pi r^2\) - площадь витка), а суммарный поток через все витки, т.е. поток через соленоид \(\Phi = N \Phi_1\) .
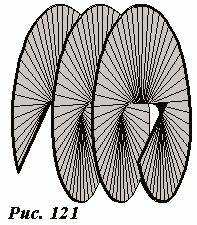
Часто для суммарного потока через катушку употребляют специальный термин – потокосцепление \(\Psi = N \Phi_1\) , однако мы в дальнейшем будем говорить о потоке через катушку, так как, во-первых, данная величина нас интересует для вычисления ЭДС в катушке, которая очевидно равна сумме ЭДС во всех витках; во-вторых, легко вообразить винтовую поверхность, опирающуюся на спиралевидную обмотку (Рис. 121), поток через которую и требуется подсчитать. К слову - эта поверхность называется геликоид.
Используя формулу (4) для индукции поля, запишем выражение для магнитного потока через обмотку
Как и следовало ожидать, этот поток пропорционален силе тока в соленоиде, коэффициент пропорциональности, т.е. индуктивность соленоида равна
где \(V = lS\) - объем соленоида.
Как следует из полученной формулы, индуктивность соленоида пропорциональна магнитной проницаемости сердечника. Это и понятно, токи намагничивания могут существенно усилить магнитное поле, а индуцированное электрическое поле создается любым переменным магнитным полем, не зависимо от того, что является его источником – токи проводимости, или токи намагничивания.
Для изготовления катушек с большой индуктивностью используют сердечники, изготовленные из ферромагнетиков с большой магнитной проницаемостью.
Используя формулу (6) для индуктивности соленоида, выразим размерность магнитной постоянной [μ0] = [L]/([n]2·[V]) = Гн/(м-2·м3) = Гн/м - именно эта размерность приводится в различных справочниках.
Примечания
- ↑ Повторим, что аксиомы физики обосновываются экспериментальными данными, в отличие от аксиом математики.
- ↑ С точки рения науки чрезвычайно интересен вопрос, что такое «сейчас», какие события можно считать одновременными, что такое прошлое, настоящее и будущее. Эта философская проблема рассматривается в теории относительности, пока же мы употребляем эти термины в обыденном житейском смысле.
- ↑ Все-таки, наверно, лучше говорить не о пространственной точке, а малой пространственной области.