Слободянюк А.И. Физика 10/16.10

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.10 Сверхпроводники в магнитном поле.

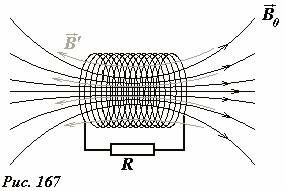
При изучении различных типов проводимости мы упоминали о сверхпроводниках – веществах, электрическое сопротивление которых в определенных условиях строго равно нулю. В электрических цепях, состоящих из сверхпроводников, наведенный электрический ток может существовать сколь угодно долго даже при отсутствии источников ЭДС. Сейчас нас по-прежнему интересует, главным образом, превращения энергии в электромагнитных явлениях, поэтому с помощью сверхпроводящих цепей мы можем обсудить эти процессы в цепях без источника энергии. Сначала рассмотрим поведение обычной не сверхпроводящей короткозамкнутой катушки-соленоида во внешнем переменном магнитном поле (Рис. 167). Обозначим L - индуктивность соленоида; R - полное электрическое сопротивление контура, состоящего из соленоида и проводника, соединяющего его концы. Пусть эта катушка помещена во внешнее магнитное поле \(~\vec B_0\), изменяющееся со временем. При изменении этого поля, возникнет вихревое электрическое поле, которое приведет к появлению электрического тока в рассматриваемой цепи. ЭДС индукции, возникающей при изменении внешнего поля, определяется законом Фарадея

\(~\varepsilon_0 = - \frac{\Delta \Phi_0}{\Delta t}\) , (1)

где Ф₀ - магнитный поток внешнего поля \(~\vec B_0\) через соленоид. Возникающий индуцированный ток создаст собственное магнитное поле, которое также будет переменным, поэтому его изменение также будет создавать в цепи ЭДС, которую мы назовем ЭДС самоиндукции, ее величина равна

\(~\varepsilon_{si} = - L \frac{\Delta I}{\Delta t}\) , (2)

где I - сила тока в цепи.

Строго говоря, разделение на ЭДС индукции и ЭДС самоиндукции является достаточно условным, так как возникновение ЭДС в контуре обусловлено одной и той же причиной: изменяющееся суммарное магнитное поле порождает суммарное вихревое электрическое поле. Но так как для электрических и магнитных полей справедлив принцип суперпозиции, то наше разделение допустимо, и удобно для теоретического описания.

Используя закон Ома для полной цепи, запишем уравнение, описывающее изменение силы электрического тока в рассматриваемой цепи

\(~-\frac{\Delta \Phi_0}{\Delta t} - L \frac{\Delta I}{\Delta t} = IR\) . (3)

При заданном законе изменения потока внешнего поля Ф₀(t) это уравнение (3) (и, конечно, начальное значение тока I₀) позволяет найти закон изменения силы тока в цепи I(t).

Направление ЭДС самоиндукции определяется правилом Ленца, которой в данном случае утверждает, что магнитный поток поля \(~\vec B'\), созданного током в цепи, препятствует изменению магнитного потока внешнего поля, или ЭДС самоиндукции препятствует изменению ЭДС индукции внешнего поля. Так, например, при возрастании потока внешнего поля Ф₀, поле индуцированного тока \(~\vec B'\) будет направлено противоположно внешнему полю, а ЭДС самоиндукции противоположна ЭДС индукции. Согласно уравнению (3) разность между модулями ЭДС индукции и ЭДС самоиндукции будет определять направление возникающего электрического тока, а величина этой разности равна электрическому напряжению в цепи IR.

Допустим теперь, что весь контур (обмотка соленоида и соединяющий проводник) переведен в сверхпроводящее состояние, при котором электрическое сопротивление равно нулю. Формально, в этом случае уравнение (3) упрощается и приобретает вид

\(~-\frac{\Delta \Phi_0}{\Delta t} - L \frac{\Delta I}{\Delta t} = 0\) . (4)

Это уравнение допускает интересную интерпретацию. Вспомним, что по определению индуктивности величина \(LI = \Phi'\) равна магнитному потоку чрез контур поля, созданного электрическим током в самом контуре. Тогда из уравнения (4) следует,

\(~-\frac{\Delta (\Phi_0 + LI)}{\Delta t} = 0\) ,

то есть изменение суммарного магнитного потока через контур равно нулю, следовательно, суммарный магнитный поток через сверхпроводящий контур сохраняется:

\(~\Phi_0 + LI = \operatorname{const}\) . (5)

Это правило широко используется при решении различных задач. Например, такой: Сверхпроводящий контур площадью S и индуктивностью L, помещают в однородное магнитное поле индуктивности B, силовые линии которого перпендикулярны плоскости контура. Чему равна сила индуцированного тока в контуре, если до помещения контура в поле ток в нем отсутствовал?

Решение этой задачи элементарно: так как магнитный поток через контур остается неизменным, и первоначально был равен нулю, то справедливо соотношение \(SB + LI = 0\), из которого находим

\(~I = -\frac{SB}{L}\) . (6)

Не смотря на постоянное использование этого правила, оно не является строгим. Более того, оно является внутренне противоречивым: действительно, если магнитный поток остается постоянным, то в контуре не может появиться ЭДС, почему же тогда в нем возникает электрический ток? Если переменное внешнее поле создает электрическое поле, и переменное поле электрического тока (не понятно, откуда появившегося) создает противоположно направленное такое же по модулю поле, то какая сила заставит двигаться электроны? Логично допустить, что все-таки ЭДС индукции должна быть чуть-чуть больше ЭДС самоиндукции |ε_ind| - |ε_si| > 0. В обычном контуре причина такой разности понятна – наличие электрического сопротивления (см. уравнение (4)). В случае сверхпроводящего контура эта причина отсутствует, однако, в случае сверхпроводников само уравнение (4), строго говоря, неприменимо. Напомним, что закон Ома описывает установившийся режим протекания электрического тока, когда сила, действующая на заряженные частицы со стороны электрического поля, уравновешивается силой сопротивления, пропорциональной скорости движения частиц. Если же силы сопротивления отсутствуют, то и установившегося режима движения нет! Поэтому в этом случае для описания движения электронов необходимо пользоваться уравнением, описывающим нестационарный, переходной процесс движения. Воспользуемся уравнением второго закона Ньютона для движения электрона

\(~m \frac{\Delta \upsilon}{\Delta t} = eE_{ind} - eE_{si}\) , (7)

где E_ind, E_si - напряженности электрических полей, созданных изменяющимися внешним магнитным полем и полем электрического тока (индукции и самоиндукции). Как следует из этого уравнения, напряженность поля индукции превышает напряженность поля самоиндукции, на величину пропорциональную массе электрона. Таким образом, мы нашли физическую причину различия этих полей – инертность носителей тока. Учет этого фактора приводит к появлению некоторой поправки к решению подобных задач. В большинстве практически значимых случаев эта поправка крайне мала (что обусловлено малой массой электронов) и в расчетах ею можно пренебречь. Однако именно этот фактор определяет само существование описываемых процессов, иными словами, в рамках этого приближения решить задачу можно, но объяснить процесс нельзя.

Пояснив смысл и рамки применимости установленного правила (5), мы в дальнейшем будем им постоянно пользоваться.

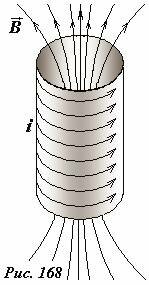
Вернемся к описанию превращений энергии в сверхпроводящем контуре при изменении его размеров. Чтобы упростить теоретическое описание и выделить наиболее существенные стороны этого описания, заменим соленоид длинным сверхпроводящим круговым цилиндром радиуса r₀ и длиной l, по поверхности которого протекает однородный электрический ток с линейной плотностью i₀ (Рис. 168).

Интересно, а как можно возбудить электрический ток по поверхности такого цилиндра?

Понятно, что для этого необходимо использовать переменное магнитное поле. Если сверхпроводник внести в магнитное поле, то в нем индуцируются электрические токи, однако, если отключить внешнее поле, то электрические токи исчезнут: посмотрите еще раз на уравнение (5) – значение силы тока однозначно определяется значением магнитного потока внешнего поля. Тем не менее, создать незатухающий ток в проводнике в отсутствии внешнего поля возможно. Для этого необходимо поместить вещество, не находящееся в сверхпроводящем состоянии, в магнитное поле. При этом благодаря электрическому сопротивлению индуцированные токи быстро затухнут. После этого проводник необходимо перевести в сверхпроводящее состояние (охлаждая его), когда он находится в постоянном поле (при этом токи также не возникнут, так как магнитное поле постоянно). Наконец, после этого можно отключить магнитное поле (или просто вынести тело из области поля), при этом уменьшающееся поле возбудит незатухающий электрический ток в сверхпроводнике.

Постоянный электрический ток, текущий по боковой поверхности, создает внутри цилиндра однородное магнитное поле (краевыми эффектами по-прежнему пренебрегаем), индукция которого равна

\(~B_0 = \mu_0 i\) . (8)

Это магнитное поле взаимодействует с токами на поверхности, со стороны поля на поверхность действует давление, равное плотности энергии магнитного поля

\(~p = \frac{B^2}{2 \mu_0}\) , (9)

где B - индукция поля внутри цилиндра.

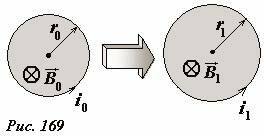
Пусть под действием этого давления цилиндр расширился так, что его радиус увеличился и стал равным r₁ (Рис. 169). Так как поверхность сверхпроводящего цилиндра при расширении двигалась в магнитном поле, то сила текущего тока изменилась. Величину тока и индукцию создаваемого им магнитного поля можно найти на основании установленного правила о постоянстве магнитного потока, которое в данном случае приводит к соотношению

\(~\pi r^2_0 B_0 = \pi r^2_1 B_1\) , (10)

из которого определим индукцию поля после расширения

\(~B_1 = B_0 \frac{r^2_0}{r^2_1}\) . (11)

Так как индукция поля, созданного током, пропорциональна линейной плотности тока (8), то аналогичное соотношения справедливо и для сил токов

\(~i_1 = i_0 \frac{r^2_0}{r^2_1}\) . (12)

Как и следовало ожидать, сила тока по поверхности и индукция поля при расширении цилиндра уменьшаются. Найдем изменение энергии поля (с учетом уменьшения плотности энергии, но увеличения занятого им объема)

\(~\Delta W = W_1 - W_0 = \frac{B^2_1}{2 \mu_0} V_1 - \frac{B^2_0}{2 \mu_0} V_0 = \frac{B^2_0}{2 \mu_0} V_0 \left( \left( \frac{r^2_0}{r^2_1} \right)^2 \frac{r^2_1}{r^2_0} - 1 \right) = \frac{B^2_0}{2 \mu_0} V_0 \left( \frac{r^2_0}{r^2_1} - 1 \right)\) . (13)

Проведенный расчет показывает, что энергия магнитного поля уменьшилась. Уменьшение энергии поля связано с работой, совершенной полем по растяжению цилиндра. При изменении радиуса цилиндра изменяется давление поля на его стенки, поэтому будем считать изменение радиуса Δr настолько малым (Δr << r₀), что изменением давления при этом можно пренебречь. В таком приближении работа поля будет равна

\(~\delta A = p_0 \Delta V = \frac{B^2_0}{2 \mu_0} \pi l ((r_0 + \Delta r)^2 - r^2_0) \approx \frac{B^2_0}{2 \mu_0} 2 \pi l r_0 \Delta r\) , (14)

при выводе мы пренебрегли малой величиной (Δr)². С таким же приближением найдем изменение энергии поля (13)

\(~\Delta W = \frac{B^2_0}{2 \mu_0} \pi l r^2_0 \left( \frac{r^2_0}{(r_0 + \Delta r)^2} - 1 \right) = \frac{B^2_0}{2 \mu_0} \pi l r^2_0 \left(\left(1 + \frac{\Delta r}{r_0} \right)^{-2} - 1 \right) \approx -\frac{B^2_0}{2 \mu_0} \pi l r^2_0 2 \frac{\Delta r}{r_0}\) , (15)

здесь использована приближенная формула \((1 + \xi)^{-2} \approx 1 - 2 \xi\) , справедливая при малых ξ.

Мы доказали, что уменьшение энергии поля равно работе по расширению цилиндра, которая в свою очередь равна увеличению его потенциальной энергии деформации. Таким образом, закон сохранения энергии выполняется и в этом случае.

Можно строго доказать, что этот вывод справедлив и при произвольном, а не только малом увеличении радиуса цилиндра, только в этом случае для прямого расчета работы необходимо выполнить операцию интегрирования.

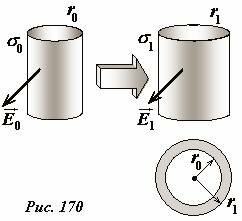
Рассмотрим аналогичную электростатическую систему: равномерно заряженный цилиндр расширяется под действием сил электростатического отталкивания. В этом случае электрическое поле расположено вне цилиндра, внутри него отсутствует. При расширении цилиндра часть электрического поля исчезает, в том объеме ΔV, на который возрос объем цилиндра при малом увеличении радиуса от r₀ до r₁. Вне этого пространства структура поля и его величина не изменяется. Поэтому изменение энергии поля при расширении цилиндра просто равно энергии, заключенной в этом «исчезнувшем» объеме между исходным и конечным положением поверхности цилиндра, то есть \(\Delta W = -w \Delta V\) , где w - объемная плотность энергии в этой части пространства. Работа, совершенная полем по расширению цилиндра равна произведению давления поля на изменение объема цилиндра \(\delta A = p \Delta V\). Так давление, равно плотности энергии \(p = w\), то эта работа в точности равна уменьшению энергии поля. Итак, мы пришли к тому же выводу: часть энергии поля перешла в энергию деформации цилиндра. Только в этом случае расчет гораздо проще и легко может быть обобщен на произвольное заряженное проводящее тело при его произвольной деформации.

Примечания

Следующая страница