Слободянюк А.И. Физика 10/16.11
§16. Превращение энергии в электрических и магнитных явлениях
16.11 Перенос энергии в электромагнитном поле.
Мы рассмотрели ряд примеров превращения различных форм энергии в электрических и магнитных явлениях и показали, что собственная энергия поля играет существенную роль в этих процессах. Если электрические и магнитные поля изменяются со временем, то неизбежно должна происходить передача энергии посредством самого электромагнитного поля. Иными словами, мы должны предположить, что электромагнитное поле не только обладает энергией, но и способно ее переносить и передавать другим телам, в которых она может преобразовываться в другие формы - тепловую, механическую и т.д. Для подтверждения этой гипотезы необходимо выразить количество передаваемой энергии через характеристики полей (напряженность электрического поля и индукцию магнитного поля). В данном разделе мы рассмотрим серию примеров такого описания переноса энергии.
16.11.1 Возрастание энергии магнитного поля.
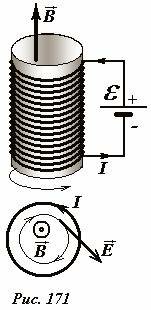
Рассмотрим механизм передачи энергии изменяющемуся магнитному полю. Для этого в очередной раз возьмем длинный соленоид радиуса r и длиной l, подключенный к источнику ЭДС (Рис. 171). Внутри соленоида магнитное поле является однородным и его индукция равна
где I - сила тока в обмотке соленоида, n - плотность ее намотки. При изменении силы тока будет изменяться индукция магнитного поля и, следовательно, его энергия. Энергию поля W представим как произведение плотности энергии \(~w = \frac{B^2}{2 \mu_0}\) на объем соленоида
Теперь изменение энергии поля можно выразить через изменение индукции поля
где использована формула \(\Delta (B^2) = 2 B \Delta B\).
Теперь попытаемся выразить это изменение энергии через характеристики полей, существующих внутри соленоида. Вспомним, что при изменении магнитного поля возникает вихревое электрическое поле (явление электромагнитной индукции). Для определенности направления векторов напряженности электрического поля на рисунках соответствуют возрастанию индукции магнитного поля. Согласно закону Фарадея циркуляция вектора напряженности электрического поля по любому контуру равна скорости изменения магнитного потока через этот контур:
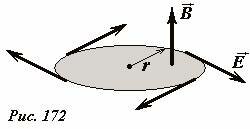
Так как магнитное поле является однородным и осесимметричным, то силовые линии электрического поля являются окружностями с центрами на оси соленоида. Поэтому в качестве контура, к которому применим уравнение (4), возьмем окружность радиуса r, непосредственно примыкающую к внутренней поверхности соленоида. На этой окружности вектор напряженности электрического поля \(~\vec E\) постоянен по модулю и направлен по касательной (Рис. 172), поэтому его циркуляция равна произведению модуля вектора на длину этой окружности \(\Gamma_E = 2 \pi r E\) . Вектор индукции магнитного поля \(~\vec B\) постоянен и направлен перпендикулярно плоскости выбранного контура, поэтому магнитный поток равен произведению модуля вектора на площадь круга, ограниченного выбранной окружностью, \(\Phi_B = \pi r^2 B\). Таким образом, уравнение (4) позволяет связать напряженность электрического поля и скорость изменения магнитной индукции
Знак минус в этом уравнении говорит, что обход контуру по направлению вектора \(~\vec E\) осуществляется по часовой стрелке[1], так нас интересуют модули векторов (их направления мы изобразили на рисунках), то этот знак минус опустим.
Напряженность электрического поля пропорциональна скорости изменения магнитной индукции. Если считать, что сила тока и индукция магнитного поля изменяются не слишком быстро, то изменением напряженности электрического поля можно пренебречь, то есть считать его постоянным. Это замечание является строгим, если сила тока в соленоиде возрастает по линейному закону.
Из уравнения (5) выразим
и подставим в формулу (3) для изменения энергии поля
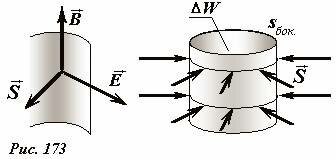
Теперь изменение энергии магнитного поля внутри объема соленоида оказалось выраженным через характеристики полей в точках, находящихся непосредственно на границе рассматриваемой области. Обратим внимание, что на этой границе (внутренней поверхности соленоида) векторы \(~\vec E\) и \(~\vec B\) (Рис. 173) взаимно перпендикулярны и направлены касательно к этой поверхности.
Введем вектор (пока как математическое обозначение[2])
пропорциональный векторному произведению векторов \(~\vec E\) и \(~\vec B\). Во всех точках внутренней поверхности соленоида этот вектор направлен по нормали и внутрь рассматриваемого объема (Рис. 173). В формуле (6) явным образом присутствует модуль этого вектора; далее, величина \(s_{bok} = 2 \pi r l\) равна площади внутренней поверхности, поэтому изменение энергии магнитного поля в (6) представлено через поток введенного вектора \(~\vec S\) через поверхность, рассматриваемый объем поля ограничивающую
На основаниях цилиндра, ограничивающего выделенный объем, вектор \(~\vec S\) не имеет нормальной составляющей, поэтому здесь его поток равен нулю.
Теперь вектор \(~\vec S\) приобретает наглядный физический смысл: его модуль равен количеству энергии, перетекающей через площадку единичной площади, перпендикулярную этому вектору, в единицу времени, а его направление указывает направление переноса энергии электромагнитного поля
Этот вектор получил название вектор Пойтинга, в честь английского ученого А. Пойтинга, который и ввел его в науку. Также этот вектор называют вектором плотности потока энергии.
Теперь наша идея о переносе энергии поля сами полем получила математическое воплощение: скорость изменения энергии магнитного поля в некотором объеме равно потоку[3] вектора Пойтинга через поверхность, ограничивающую этот объем. В данном случае положительным считается поток направленный внутрь поверхности.
При уменьшении тока в соленоиде направление вектора \(~\vec B\) не изменяется, а направление вектора \(~\vec E\) изменяется на противоположное. Поэтому направление вектора плотности потока энергии \(~\vec S\) также изменяется на противоположное – теперь он будет направлен наружу от рассматриваемого объема. Такое изменение логично – энергия поля уменьшается, поэтому она «вытекает» из выделенного объема.
16.11.2 Возрастание энергии электрического поля.
Рассмотрим теперь механизм передачи энергии изменяющемуся электрическому полю.
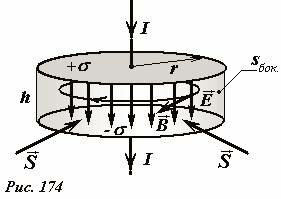
Для этого возьмем плоский конденсатор с круглыми параллельными пластинами радиуса r, находящимися на малом расстоянии h друг от друга (Рис. 174). Электрическое поле между пластинами можно считать однородным, вектор его напряженности \(~\vec E\) перпендикулярен пластинам, его модуль равен
где σ - поверхностная плотность заряда на пластинах. Полная энергия электрического поля в конденсаторе равна произведению плотности энергии \(~w = \frac{\varepsilon_0 E^2}{2}\) на объем конденсатора \(V = \pi r^2 h\):
При изменении зарядов на платинах (опять для определенности будем считать, что заряды возрастают) напряженность электрического поля и его энергия изменяются. Изменение этой энергии описывается формулой
Выразим это изменение через характеристики полей на границе выделенного объема (в данном случае на цилиндрической боковой поверхности, ограничивающей внутренне пространство между обкладками).
При изменении со временем электрического поля возникает поле магнитное (это явление мы назвали токами смещения). Для определения его индукции воспользуемся уравнением Максвелла: циркуляция вектора магнитной индукции по любому контуру пропорциональна скорости изменения потока вектора напряженности электрического поля через этот контур (при отсутствии токов, пересекающих контур):
Ранее мы описывали структуру магнитного поля в рассматриваемой системе и показали, что его силовые линии являются окружностями с центрами на оси конденсатора[4]. Поэтому в качестве контура выберем окружность радиуса r с центром на оси конденсатора. На этой окружности вектор индукции \(~\vec B\) постоянен по модулю и направлен по касательной, поэтому его циркуляция рана произведению модуля вектора на длину окружности. Вектор напряженности \(~\vec E\) постоянен, поэтому его поток через выделенный контур равен произведению модуля на площадь круга, ограниченного выбранным контуром. Таким образом, для этого контура теорема (4) приводит к уравнению
из которого выразим
и подставим в формулу (3)
Здесь также изменение энергии электрического поля представляется в виде потока вектора Пойтинга
Действительно, на рассматриваемой поверхности векторы \(~\vec B\) и \(~\vec E\) перпендикулярны друг другу и направлены касательно к поверхности, поэтому вектор \(~\vec S\) перпендикулярен поверхности и направлен внутрь рассматриваемого объема (см. Рис. 174). Поэтому произведение его модуля \(~S = \frac{EB}{\mu_0}\) на площадь боковой поверхности \(s_{bok} = 2 \pi r l\) есть поток этого вектора, поэтому выражение (5) можно представить в виде
Отмечаем, что у поверхности пластин конденсатора вектор \(~\vec S\) направлен вдоль пластин, поэтому здесь его поток равен нулю. Итак, мы приходим к заключению: скорость изменение энергии электрического поля в некотором объеме равно потоку вектора Пойтинга через поверхность, ограничивающую данный объем. Как и ранее положительным считаем поток направленный внутрь поверхности.
Вдумайтесь еще раз в сделанный вывод и посмотрите на рисунок: мы показали, что энергия внутрь конденсатора проникает в «щелки» между пластинами из окружающего пространства, а не «стекает» с пластин (как в соленоиде, где вектор плотности потока направлен от обмотки). Значит, она должна каким-то образом обогнуть края пластин, но ее точный путь описать также сложно, как и краевые эффекты.
Легко показать, что при уменьшении заряда на пластинах, энергия «вытекает» из конденсатора, так как в этом случае вектор Пойтинга направлен наружу из конденсатора.
16.11.3 Перенос энергии при выделении теплоты.
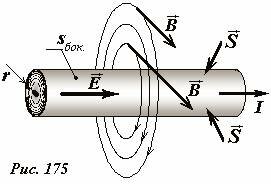
Протекание электрического тока по проводнику сопровождается выделением теплоты. Покажем, что и в этом случае энергия поступает к нагревающемуся проводнику через электромагнитное поле. Пусть электрический ток силой I протекает по однородному цилиндрическому проводнику радиуса r и длины l (Рис. 175). За промежуток времени Δt в проводнике выделяется количество теплоты, определяемое законом Джоуля-Ленца
где R - электрического сопротивление проводника. Выразим эту величину через характеристики электромагнитного поля в проводнике.
Точнее мы будем рассматривать поля в точках находящихся под боковой поверхностью проводника, примыкающих к ней изнутри проводника. Дело в том, что непосредственно на поверхности проводника распределяются поверхностные заряды, создающие поле внутри проводника. Поэтому внутри проводника электрическое поле существует и заставляет двигаться заряженные частицы, а вне проводника электрическое поле отсутствует, так сам проводник остается электрически нейтральным. Магнитное поле существует как внутри так вне проводника с током.
Электрическое поле внутри проводника является однородным, вектор его напряженности \(~\vec E\) направлен вдоль оси проводника, а его модуль может быть определен из закона Ома для участка цепи:
где Δϕ - разность потенциалов между концами проводника (приложенное электрическое напряжение). Электрический ток создает магнитное поле, силовые линии которого образуют концентрические окружности с центрами на оси проводника. Индукция этого поля непосредственно у поверхности определяется по формуле
Выражая значения силы тока через напряженность электрического поля из формулы (2) \(IR = El\) и индукцию магнитного поля из формулы (3) \(~I = \frac{2 \pi r B}{\mu_0}\) , преобразуем выражение (1) к виду
Таким образом, мощность выделяющейся теплоты равно потоку вектора Пойтинга
через боковую поверхность проводника, площадь которой равна \(s_{bok} = 2 \pi r l\).
Обратите внимание, что и в этом случае векторы \(~\vec E\) и \(~\vec B\) перпендикулярны друг другу и направлены по касательным к боковой поверхности, поэтому вектор \(~\vec S\) перпендикулярен поверхности и направлен внутрь проводника. Таким образом, заключаем: количество теплоты, выделяющейся в некотором объеме, в единицу времени равно потоку вектора Пойтинга через поверхность, ограничивающую данный объем.
При изменении направления тока изменяться на противоположные направления векторов \(~\vec E\) и \(~\vec B\), а направление вектора потока энергии \(~\vec S\) останется неизменным. Очевидно, что количество выделяющейся теплоты не зависит от направления тока, и при любом направлении тока энергия должна «втекать» в проводник, вследствие чего и направление потока энергии не зависит от направления тока.
Опять мы пришли к неожиданному выводу: энергия втекает в проводник из окружающего пространства через боковую поверхность. То есть энергия электрического тока передается не по проводам, в проводах она только теряется. Так при отсутствии электрического сопротивления отсутствует электрическое поле, поэтому отсутствует поток энергии направленный внутрь проводника.
Зачем же тогда они нужны эти провода? Оказывается, их роль заключается в создании электромагнитного поля нужной конфигурации, такой, чтобы поле в окружающем проводник пространстве могло передавать энергию потребителю.
16.11.4 Перенос энергии при совершении механической работы.
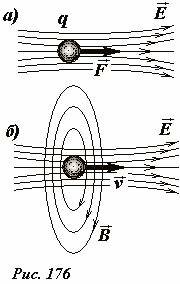
На неподвижную заряженную частицу, находящуюся в стационарном электрическом поле действует некоторая сила \(~\vec F\). Если частица неподвижна, то эта сила работы не совершает, поэтому никакой передачи энергии ей не требуется (Рис. 176а). Если же частицу освободить, то под действием силы \(~\vec F\) она придет в движение, ее скорость начнет возрастать, поэтому будет расти и ее кинетическая энергия. В этом случае частица должна получать энергию извне. Движущаяся заряженная частица будет создавать магнитное поле (Рис. 176б). Совокупность взаимно перпендикулярных электрического и магнитного полей может переносить энергию и передавать ее частице. Таким образом, возникающее при движении частицы магнитное поле создает механизм передачи энергии от поля к частице, превращения энергии поля в кинетическую энергию движущейся частицы.
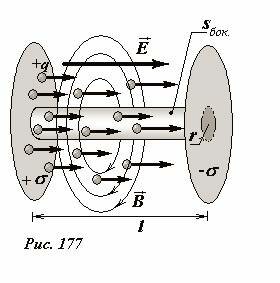
Для количественного подтверждения этих качественных рассуждений, рассмотрим процесс передачи энергии в установке (Рис. 177), в которой легко найти значения действующих полей.
Между двумя параллельными пластинами создано однородное стационарное электрическое поле, напряженности \(~\vec E\). Одна из пластин испускает с начальной скоростью υ0 заряженные частицы, каждая из которых имеет массу m и несет электрический заряд q.
Рассматриваемое устройство является аналогом электровакуумных приборов, в которых разогретый катод испускает электроны, ускоряемые затем электрическим полем.
Изменение кинетической энергии одной частицы при ее пролете между пластинами равно работе электрического поля
Мысленно выделим в потоке частиц узкий цилиндр радиуса r, ось которого перпендикулярна пластинам и параллельна направлению вектора напряженности \(~\vec E\). Пусть за время Δt с площадки, на которую опирается выбранный цилиндр, испускается δN частиц. За этот же промежуток времени столько же частиц проходят через любое поперечное сечение рассматриваемого цилиндра, столько же частиц достигают второй пластины. Следовательно, изменение кинетической энергии всех частиц за промежуток времени Δt равно
Найдем зависимость между числом испущенных частиц и индукцией создаваемого ими магнитного поля. Движущиеся заряженные частицы образуют электрический ток. За время Δt через любое поперечное сечение цилиндра проходит δN частиц, которые переносят электрический заряд \(\Delta q = q \Delta N\), поэтому сила электрического тока, протекающего по выделенной трубке, равна
В данном устройстве сила тока не зависит от напряженности электрического поля, а полностью определяется интенсивностью испускания – при любой напряженности все испущенные частицы достигают противоположной пластины: число испущенных в единицу времени частиц, равно числу частиц попавших на противоположную пластину. Кроме того, частицы движутся с ускорением, их скорость υ постоянно растет, но сила электрического тока по длине трубки не изменяется – с ростом скорости уменьшается их концентрация n, а произведение nυ, которое определяет силу тока, остается постоянным.
Индукция магнитного поля на границе рассматриваемого цилиндра равна
Из этой формулы выразим значение \(~q \delta N = \frac{B}{\mu_0} 2 \pi r \Delta t\) и подставим его в выражение (2), в результате чего получим формулу для изменения кинетическое энергии потока частиц, выраженное через характеристики поля
В очередной раз мы получили, что скорость изменения энергии (в данном случае кинетической) потока частиц равно произведению модуля вектора Пойтинга \(~\vec S = \frac{\vec E \times \vec B}{\mu_0}\) на площадь боковой поверхности рассматриваемого цилиндра \(s_{bok} = 2 \pi r l\). Учитывая, что векторы \(~\vec E\) и \(~\vec B\) перпендикулярны друг другу и направлены по касательным к боковой поверхности, а вектор \(~\vec S\) перпендикулярен поверхности и направлен внутрь проводника, заключаем, что скорость изменение кинетической энергии заряженных частиц в некотором объеме равно потоку вектора Пойтинга через поверхность, ограничивающую данный объем.
Рассмотренный пример аналогичен выделению теплоты при прохождении электрического тока, так как в обоих случаях электрическое поле совершает работу над заряженными частицами, только в одном случае эта работа приводит к увеличению кинетической энергии, а в другом расходуется на преодоление сил сопротивления (в результате чего выделяется теплота). Но это различие относится к области механики, а не электродинамики.
16.11.5 Теорема о потоке энергии электромагнитного поля.
Мы рассмотрели четыре примера переходов энергии из одной формы в другую с участием электромагнитного поля. Выбор этих примеров был обусловлен, главным образом, их простотой – в каждом случае нам удалось независимо рассчитать изменение энергии системы и характеристики полей, существующих на границе рассматриваемой области. В этих процессах часто тяжело определить, что является причиной, что – следствием: с одной стороны наличие скрещенных полей обеспечивает поток энергии, а, с другой, сами процессы формируют нужную конфигурацию электромагнитного поля.
Далее мы показали, что изменение энергии (в любой форме – энергии поля, внутренней, тепловой энергии, механической энергии) рассматриваемой системы можно представить как поток энергии через границу этой системы. Оказалось, что во всех случаях передачи энергии обязательно присутствие непараллельных электрического и магнитного полей. Количественной характеристикой процесса переноса энергии во всех случаях выступает вектор Пойтинга (вектор плотности потока энергии)
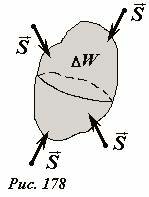
Обобщая полученные результаты, закон сохранения энергии можно сформулировать в виде[5]: скорость изменения энергии системы равно потоку вектора Пойтинга через поверхность, ограничивающую данную систему (Рис. 178), причем положительным считается поток, направленный внутрь рассматриваемого объема.
Конечно, это утверждение справедливо, если нет других механизмов передачи энергии данной системе извне: над ней не совершается механическая работа, нет потоков теплоты.
Заметим, что энергия может и «вытекать» из рассматриваемого объема, когда система обдает энергию внешним телам, например, совершает над ними работу. В этом случае поток энергии следует считать отрицательным.
Полученная формулировка закона сохранения энергии вполне очевидна. Ее аналогом может служить утверждение, что «в сосуде содержится столько жидкости, сколько вы ее туда налили».
Вектор плотности потока энергии \(~\vec S\) определен во всех точках пространства, в котором существует электромагнитное поле, поэтому с математической точки зрения его описание задается векторным полем, для которого применимы все математические операции: поток, циркуляция и т. д. Так поток вектора \(~\vec S\) через малую площадку определяется традиционно, как произведение нормальной составляющей вектора на площадь площадки (Рис. 179)
где α - угол между векторами нормали \(~\vec n\) и плотности потока энергии \(~\vec S\). Чтобы вычислить поток через произвольную поверхность, необходимо разбить ее на малые участки Δsi, найти поток через каждую такую площадку и просуммировать их по всем площадкам (Рис. 180)
Напомним, что традиционно для замкнутой поверхности положительной считается внешняя нормаль. Чтобы не нарушать традицию, при определении полного потока энергии через замкнутую поверхность, также будем считать положительным поток, направленный наружу, то есть «вытекающий» из рассматриваемого объема. При таком определении теорема о потоке энергии звучит следующим образом: поток вектора Пойтинга (вектора плотности потока энергии электромагнитного поля) через любую замкнутую поверхность равен скорости уменьшения энергии, заключенной внутри данной поверхности
Как и другие теоремы о потоках, данная теорема также широко используется при описании и изучении электромагнитных явлений, в дальнейшем мы также будем обращаться к ней.
Примечания
- ↑ Вспомните, что положительным направлением обхода условились считать движение «против часовой стрелки».
- ↑ К сожалению, такое обозначение этого вектора является традиционным и общепринятым, поэтому в дальнейшем для обозначения площади мы будем использовать s - «эс малое».
- ↑ Лучше было бы сказать: равно потоку (в смысле математической операции) вектора плотности потока (а это имя вектора), но эта фраза звучит не очень хорошо...
- ↑ Сравните структуры полей в соленоиде и конденсаторе – электрическое и магнитное поля просто поменялись местами, поэтому далее можно просто переписать предыдущий раздел с указанной заменой, что далее и сделано...
- ↑ Эту формулировку можно доказать на основе уравнений Максвелла в самом общем случае, произвольных систем, произвольных электромагнитных полей. Наши примеры следует считать только иллюстрациями этой общей формулировки, а не ее доказательством.