Слободянюк А.И. Физика 10/16.5

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

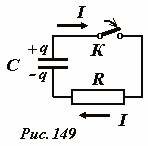
16.5 Разрядка конденсатора.

Если обкладки заряженного конденсатора соединить проводником (сопротивление которого обозначим R), то заряды начнут перетекать с одной обкладки на другую, в результате чего конденсатор будет разряжаться. Направление тока в этом случае, очевидно, противоположно направлению тока при зарядке конденсатора. Так как в рассматриваемом контуре нет источника сторонних сил, то сумма напряжений на конденсаторе и резисторе равна нулю (свойство потенциальности электростатического поля)\[U_C + U_R = 0\]. Используя выражения для соответствующих напряжений, получим уравнение

\(~\frac{q}{C} + IR = 0\) . (1)

выражая силу тока через изменение заряда, окончательно получим требуемое уравнение

\(~R \frac{\Delta q}{\Delta t} = -\frac{1}{C}q\) . (2)

Интересно, что аналогичное уравнение можно получить непосредственно и для силы тока. Для этого с помощью уравнения (1) запишем уравнение для малых изменений силы тока и заряда \(~\frac{\Delta q}{C} + R \Delta I = 0\), разделив которое на малый промежуток времени, получим

\(~\frac{\Delta I}{\Delta t} = -\frac{1}{RC}t\) . (3)

Это уравнение полностью совпадает с уравнением (3) предыдущего раздела, описывающим изменение силы тока при зарядке конденсатора, поэтому его решение будет таким же, как показано на рис. 146. Единственное отличие заключается в начальных условиях. В данном случае значение силы тока в начальный момент времени определяется уравнением (1) и равно \(~I_0 = \frac{q_0}{RC}\), где q₀ - начальный заряд конденсатора.

Для описания процессов преобразования энергии, умножим уравнение (1) на малое изменение заряда Δq_i и просуммируем по всему процессу разрядки конденсатора (в котором заряд уменьшается от начального значения q₀ до нуля)

\(~\sum_i \frac{q_i}{C} \Delta q_i + \sum_i I_i R \Delta q_i = 0\) .

В полученном выражении смысл каждого слагаемого очевиден: \[~\sum_i \frac{q_i}{C} \Delta q_i = \frac{1}{2C} \Delta (q^2) = -\frac{q^2_0}{2C}\] - изменение энергии конденсатора, модуль которого равен его начальной энергии; \[~\sum_i I_i R \Delta q_i = \sum_i I^2_i R \Delta t\] - количество теплоты, выделившейся на резисторе.

Таким образом, энергия электрического поля, заключенная в конденсаторе, превращается в тепловую энергию. Закон сохранения энергии при этом, конечно, выполняется.

Количество выделившейся теплоты можно подсчитать аналогично, как в случае зарядки конденсатора, (только с другим значением начальной силы тока),

\(~Q = \sum_i (I(t_i))^2 R \Delta t_i = \frac{1}{2} I^2_0 R \tau = \frac{1}{2} \left ( \frac{q_0}{RC} \right )^2 R \cdot RC = \frac{q^2_0}{RC}\) ,

что в точности равно начальной энергии конденсатора.

Следующая страница