Слободянюк А.И. Физика 10/16.6

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.6 Перераспределение зарядов на конденсаторах.

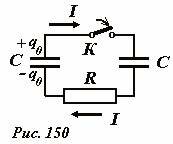
Рассмотрим еще один интересный и поучительный пример. Пусть конденсатор емкостью C , имеющий заряд q₀ подключается к другому такому же конденсатору (Рис. 150). После установления равновесия напряжения на конденсаторах станут равными, поэтому электрические заряды распределятся между ними поровну. При этом суммарная энергия конденсаторов уменьшается. Действительно, начальная энергия заряженного конденсатора равна

\(~W_0 = \frac{q^2_0}{2C}\) . (1)

После перезарядки суммарная энергия конденсаторов станет равной

\(~W_1 = 2 \frac{1}{2C} \left ( \frac{q_0}{2}\right)^2 = \frac{q^2_0}{4C}\) , (2)

то есть уменьшится в два раза. Понятно, что потери энергии электрического поля обусловлены выделением теплоты при протекании электрического тока в ходе перераспределения зарядов. Таким образом, количество выделившейся теплоты равно уменьшению энергии конденсаторов

\(~Q = W_0 - W_1 = \frac{q^2_0}{4C}\) ,

что составляет ровно половину начальной энергии.

Отметим, что величина этих потерь не зависит от сопротивления цепи, соединяющей конденсаторы – это сопротивление определяет длительность процесса перераспределения. Опять мы встречаемся с «обязательным» тепловым налогом, который и в рассмотренном случае также составляет 50%.

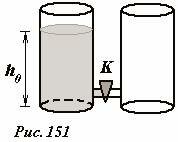
Данная задача имеет очень простую гидростатическую аналогию. Пусть два одинаковых цилиндрических сосуда соединены в нижней части трубкой с краном K (Рис. 151). Пусть первоначально в одном сосуде находится жидкость, высоту уровня которой обозначим h₀. Эта жидкость обладает потенциальной энергий в поле тяжести, равной

\(~W_0 = mgh_c = \rho S h_0 g \frac{h_0}{2} = \frac{\rho S g \cdot h^2_0}{2}\) ,

где \(h_c = \frac{h_0}{2}\) - высота центра масс жидкости, ρ - плотность жидкости, \(m = \rho S h_0\) - ее масса, S - площадь сосуда. Если открыть кран, то жидкость начнет перетекать во второй сосуд. После установления равновесия уровни жидкости в сосудах сравняются на высоте \(~\frac{h_0}{2}\), следовательно, центр масс жидкости окажется на высоте \(h_{c1} = \frac{h_0}{4}\). При этом потенциальная энергия жидкости станет равной \(~W_1 = mgh_{c1} = \frac{\rho S g \cdot h^2_0}{4}\) , то есть уменьшится в два раза. Потери энергии и в данном случае связаны с выделением теплоты при перетекании жидкости, связанной с силами вязкого трения (опять «тепловой налог»!). Если бы эти силы отсутствовали, то уровни жидкости колебались бы бесконечно долго.

Подумайте, а что будет с зарядом конденсаторов, если они изготовлены из сверхпроводников и соединены сверхпроводящими проводами!

Задания для самостоятельной работы.

1. Найдите изменение энергии поля, если конденсаторы в рассмотренной задаче имеют различные емкости.
2. Получите уравнение, описывающее изменение силы тока при перераспределении зарядов, качественно проанализируйте его решение, найдите характерное время установления равновесия в рассматриваемой цепи.

Примечания

Следующая страница