Слободянюк А.И. Физика 10/17.1

Содержание книги

Предыдующая страница

§17. Механические колебания

17.1 Периодические функции.

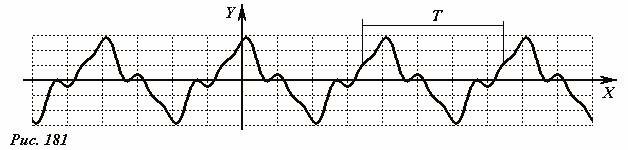
Функция F(x) называется периодической (Рис. 181), если существует такое число T, что для любого значения x справедливо выражение

\(~F(x+T) = F(x)\) . (1)

Очевидно, что подобное соотношение будет справедливо и для сдвига аргумента на 2T, 3T, .... Минимальное значение T, для которого выполняется соотношение (1) называется периодом функции.

Простейшими, и наиболее известными периодическими функциями являются тригонометрические функции синус и косинус.

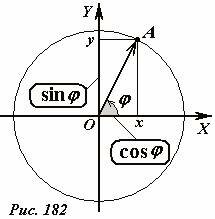
Возьмем окружность единичного радиуса с центром в начале координат (Рис. 182). Положение произвольной точки A этой окружности задается единичным радиус-вектором \(~\vec {OA}\), образующим угол φ с осью Ox. Как обычно, положительным направлением отсчета угла является направление «против часовой стрелки. Косинусом угла φ называется абсцисса x радиус-вектора точки A, синусом угла φ называется ордината y этого же вектора. Аргумент этих функций может принимать произвольные значения.

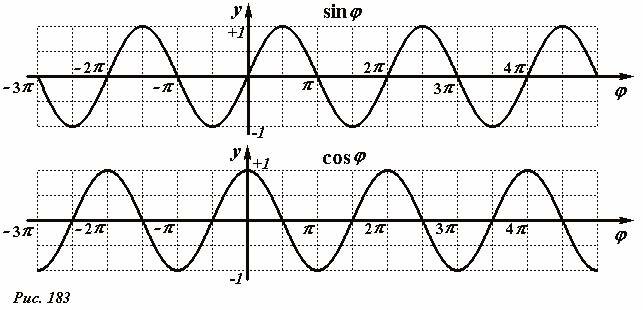
Понятно, что при изменении аргумента на полный угол 2π радиус-вектор занимает прежнее положение, поэтому периодом функций \(y = \sin \varphi\) и \(y = \cos \varphi\) является величина T = 2π. На рис. 183 приведены графики этих функций.

Заметим, что графики этих функций изображаются одной и той же кривой, которая называется синусоидой, только сдвинуты друг относительно друга на величину \(~\frac{\pi}{2}\) . Из определения тригонометрических функций и рис. 182 следуют формулы приведения

\(~\begin{matrix} \sin \left (\varphi + \frac{\pi}{2} \right) = \cos \varphi, & \sin (\varphi + \pi) = -\sin \varphi \\ \cos \left (\varphi + \frac{\pi}{2} \right) = -\sin \varphi, & \cos (\varphi + \pi) = -\cos \varphi \end{matrix}\) . (2)

Обратим также внимание, что косинус является четной функцией \(\cos (-\varphi) = \cos \varphi\) , а синус – нечетной \(\sin (-\varphi) = -\sin \varphi\).

Приведем ряд тригонометрических формул, которые нам понадобятся в дальнейшем.

Из теоремы Пифагора следует основное тригонометрическое тождество

\(~\sin^2 \varphi + \cos^2 \varphi = 1\) , (3)

из которого легко выразить одну из тригонометрических функций через другую.

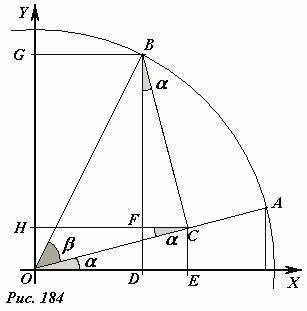
Получим формулы для синуса и косинуса суммы двух аргументов. Пусть единичный отрезок OA образует угол α с осью Ox (Рис. 184). Проведем еще один единичный отрезок OB, образующий угол β с отрезком OA и, соответственно угол (α + β) с осью Ox. Согласно определению косинус суммарного угла равен длине отрезка OD, которая равна разности длин отрезков OE и DE :

\(~\cos(\alpha + \beta) = |OD| = |OE| - |OD|\).

Рассматривая прямоугольный треугольник OBC, видим, что его катеты равны

\(~\begin{matrix} |OC| = \cos \beta \\ |BC| = \sin \beta \end{matrix}\) .

Далее, рассматривая подобные треугольники OCE и BFC, в которых один из углов равен α, находим, что

\(~\cos(\alpha + \beta) = |OD| = |OE| − |OD| = |OC| \cos \alpha - |BC| \sin \alpha = \cos \beta \cdot \cos \alpha - \sin \beta \cdot \sin \alpha\).

Таким образом, формула для косинуса суммы имеет вид

\(~\cos(\alpha + \beta) = \cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta\). (3)

Аналогично с помощью рис. 184 можно получить формулу для синуса суммы

\(~\sin(\alpha + \beta) = \sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta\). (4)

Полагая в этих формулах α = β, получим формулы для косинуса и синуса двойного аргумента:

\(~\begin{matrix} \cos 2 \alpha = \cos^2 \alpha - \sin^2 \alpha \\ \sin 2 \alpha = 2 \sin \alpha \cdot \cos \alpha \end{matrix}\) . (5)

Из первой из этих формул и основного тригонометрического тождества следую формулы «понижения степени»:

\(~\begin{matrix} \cos^2 \alpha = \frac{1}{2} (1 + \cos 2 \alpha) \\ \sin^2 \alpha = \frac{1}{2} (1 - \cos 2 \alpha) \end{matrix}\) . (6)

Используя формулу для косинуса суммы, получим формулы для преобразования произведения тригонометрических функций в сумму. Из формулы для косинуса суммы

\(~\cos(\alpha + \beta) = \cos \alpha \cdot \cos \beta - \sin \alpha \cdot \sin \beta\)

запишем формулу для косинуса разности (используя свойства четности тригонометрических функций)

\(~\cos(\alpha - \beta) = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta\).

Складывая и вычитая эти две формулы, получим, что

\(~\begin{matrix} \cos \alpha \cdot \cos \beta = \frac{1}{2} (\cos(\alpha - \beta) + \cos(\alpha + \beta)) \\ \sin \alpha \cdot \sin \beta = \frac{1}{2} (\cos(\alpha - \beta) - \cos(\alpha + \beta)) \end{matrix}\) . (7)

Покажем, как можно преобразовать линейную комбинацию синуса и косинуса \(y(\varphi) = A \sin \varphi + b \cos \varphi\). Вынесем за скобки выражение \(~\sqrt{A^2 + B^2}\):

\(~y(\varphi) = A \sin \varphi + b \cos \varphi = \sqrt{A^2 + B^2} \left( \frac{A}{\sqrt{A^2 + B^2}} \sin \varphi + \frac{B}{\sqrt{A^2 + B^2}} \cos \varphi \right)\) . (8)

Теперь коэффициенты при синусе и косинусе удовлетворяют условию

\(~\left( \frac{A}{\sqrt{A^2 + B^2}} \right)^2 + \left( \frac{B}{\sqrt{A^2 + B^2}} \right)^2 = 1\),

поэтому их можно обозначить как косинус и синус некоторого угла Δφ:

\(~\frac{A}{\sqrt{A^2 + B^2}} = \cos \Delta \varphi ; \frac{B}{\sqrt{A^2 + B^2}} = \sin \Delta \varphi\) . (9)

Следовательно, формулу (8) можно записать в виде

\(~y(\varphi) = A \sin \varphi + b \cos \varphi = \sqrt{A^2 + B^2} (\sin \varphi \cdot \cos \Delta \varphi + \sin \Delta \varphi \cdot \cos \varphi) = \sqrt{A^2 + B^2} \sin (\varphi + \Delta \varphi)\) . (10)

Таким образом, линейная комбинация синуса и косинуса одного аргумента может быть представлена как синус (или косинус) аргумента с некоторым сдвигом, величина которого определяется формулами (9).

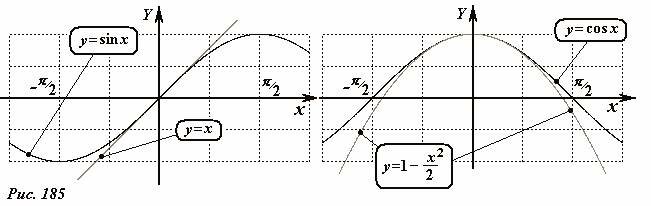
Отметим также приближенные формулы, справедливые при малых значениях аргумента (x << 1): синус малого аргумента приблизительно равен самому аргументу

\(~\sin x \approx x\) . (11)

Погрешность этой формулы составляет величину порядка x³. Геометрически эта формула означает, что длина малой форды примерно равна длине дуги, стягивающей эту хорду.

Для косинуса малого аргумента справедлива приближенная формула

\(~\cos x \approx 1 - \frac{x^2}{2}\) , (12)

погрешность которой является величиной порядка x⁴. Рис. 185 иллюстрирует эти приближенные формулы.

Наконец, приведем выражения для производных от этих функций:

производная синуса угла равна косинусу этого же угла

\(~(\sin x)' = \cos x\) , (13)

а производная косинуса равна синусу, взятому с противоположным знаком:

\(~(\cos x)' = -\sin x\) . (14)

Примечания

Следующая страница