Слободянюк А.И. Физика 10/17.2
§17. Механические колебания
17.2 Кинематика колебательного движения.
В данном разделе мы рассмотрим простейшую кинематическую модель колебательного движения материальной точки, движущейся вдоль прямой. Условия, при которых эта модель адекватно описывает реальные колебания, могут быть получены только на основании физических законов, в частности, законов динамики.
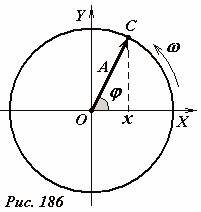
Для построения этой модели обратим внимание, что равномерное движение точки по окружности является периодическим процессом. Действительно, пусть материальная точка C движется с постоянной угловой скоростью ω по окружности радиуса A. При этом угловая координата точки будет изменяться по линейному закону
где φ0 - начальная координата точки. Не смотря на то, что угол поворота монотонно возрастает, через равные промежутки времени, равные периоду вращения \(~T = \frac{2 \pi}{\omega}\) точка возвращается в исходное положение, в котором ее кинематические характеристики (скорость, ускорение) принимают исходные значения. Если радиус-вектор точки, векторы ее скорости и ускорения изменяются по периодическому закону, то и их проекции также изменяются по периодическим законам. Иными словами, движение проекции точки на любую из осей координат является колебательным движением вдоль прямой.
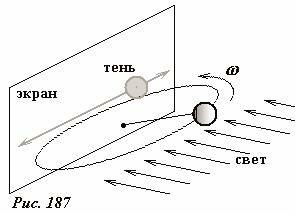
Отметим, что такое колебательное движение проекции можно наблюдать в реальном эксперименте. Для этого необходимо поместить вращающийся по окружности шарик перед плоским экраном и осветить его световым потоком, параллельным плоскости вращения (Рис. 187). В этом случае тень от шарика будет совершать колебания вдоль одной прямой.
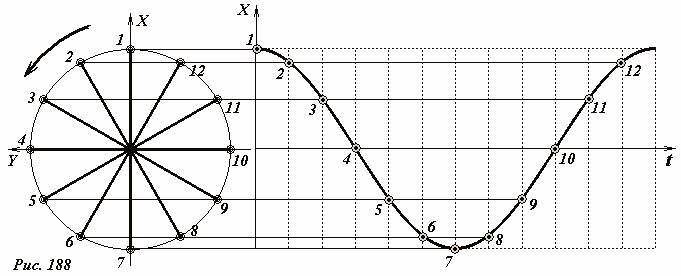
Даже будучи не знакомы с тригонометрическими функциями, достаточно легко построить график закона движения тени шарика. Для этого необходимо изобразить окружность, отметить на ней равноотстоящие точки, а затем нанести на график временной зависимости их координаты через равноотстоящие интервалы времени. (Рис. 188).
Не будем делать вид, что нам совсем незнакома ни тригонометрия, ни кинематические законы равномерного движения по окружности, и на их основании получим строгие выражения для кинематических характеристик рассматриваемой модели колебательного движения.
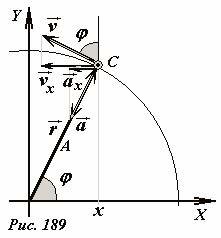
Еще раз изобразим часть окружности радиуса A, по которой движется материальная точка C (Рис. 189). Положение точки задается радиус-вектором \(~\vec r\), направленным под переменным углом φ к оси Ox. Проекция этого вектора на ось Ox равна
Учитывая, что угол поворота изменяется в соответствии с формулой (1), получим закон изменения координаты точки от времени
Движение, при котором координата точки изменяется по закону косинуса (или синуса) называется гармоническим [1] колебанием. Таким образом, при равномерном движении точки по окружности ее проекция совершает гармонические колебания.
Как следует из вида функции (3), гармоническое колебание точки определяется тремя параметрами, каждый из которых имеет наглядный смысл[2]. Параметр A называется амплитудой колебаний, он равен максимальному отклонению точки от центрального положения. Эта величина имеет ту же размерность, что и координата x, то есть размерность длины. Изменяющаяся величина \(\varphi = \varphi_0 + \omega t\) называется фазой колебания, а величина φ0 - начальной фазой.
Параметр ω называется круговой частотой колебаний. Так как период косинуса равен 2π, то при изменении аргумента косинуса на эту величину значения функции принимает прежнее значение. Это обстоятельство позволяет выразить круговую частоту через время одного колебания T (которое также называется периодом колебаний). Для этого следует учесть, что при изменении времени на период Δt = T фаза колебания изменяется на \(\Delta \varphi = \omega \Delta t = 2 \pi\), то есть \(\omega T = 2 \pi\). Таким образом, круговая частота связана с периодом колебания соотношением
Более наглядной характеристикой колебаний является обычная частота ν - число колебаний в единицу времени. Если период – это время одного колебания, то величина обратная периоду равна числу колебаний в единицу времени, то есть частоте колебаний
С помощью соотношений (4)-(5) легко связать круговую и обычную частоты колебаний
Очевидно, что круговая и обычные частоты являются размерными физическими величинами, их размерность обратная размерности времени [ω] = [ν] = [T]-1 = c-1. Для обычной частоты колебаний единица ее измерения называется Герц (сокращенно Гц): частота колебаний 1 Герц означает одно колебание в секунду.
На основании полученного соотношения (6) иногда говорят, что круговая частота колебаний равна числу колебаний за 2π секунд .Однако, по нашему мнению, такое определение является излишним, потому, что, во-первых, попробуйте точно отмерить указанное количество секунд, а, во-вторых, время не обязательно измерять в секундах. Поэтому к этой величине следует относиться как к удобной вспомогательной математической величине – если везде использовать только физически наглядную частоту колебаний ν, то во всех формулах придется дописывать множитель 2π, что приводит к необоснованному перерасходу чернил и бумаги. Также не следует искать особого наглядного смысла в фазе колебаний.
Отметим, что подобные замечания касательно угловой скорости вращения ω (аналогом которой является круговая частота) не обоснованы, так угловая скорость имеет явный физический смысл – угол поворота (измеренный в радианах) в единицу времени.
При движении по окружности вектор скорости точки направлен по касательной к окружности (см. Рис. 189), его модуль равен \(\upsilon = \omega A\) (напомним, здесь A - радиус окружности). Если проекция радиус-вектора \(~\vec r\) есть координата точки x , то проекция вектора скорости \(~\vec \upsilon\) на ту же ось будет равна скорости движения проекции. Из рисунка не сложно определить, что проекция вектора скорости на ось Ox равна \(\upsilon_x = -\upsilon \sin \varphi\). Используя выражения для модуля скорости и выражение для угла поворота, определяем, что скорость точки при гармоническом колебании (3) зависит от времени по закону
Величина \(\omega A = \upsilon_0\) равна максимальной скорости движения точки при гармонических колебаниях. Отметим также, что при гармонических колебаниях скорость точки также изменяется по гармоническому закону.
Аналогичным образом найдем ускорение точки, совершающей гармонические колебания. Так при равномерном движении по окружности ускорение точки является центростремительным, то есть вектор ускорения \(~\vec a\) направлен к центру окружности, а его модуль равен \(a = \omega^2 A\). Из рис. 189 следует, проекция вектора ускорения на выбранную ось Ox равна \(a_x = -a \cos \varphi\). Следовательно, зависимость ускорения от времени при гармонических колебаниях имеет вид
Полученные функции зависимости скорости и ускорения точки от времени можно получить непосредственно из закона движения (3). Действительно, мгновенная скорость является первой производной координаты по времени, поэтому функция (7) является первой производной от функции (3).
Аналогично зависимость ускорения от времени (8) является первой производной от скорости (7) или второй производной координаты (3).
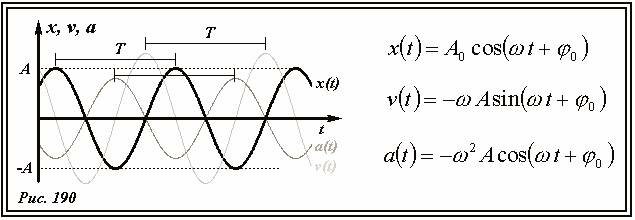
На рис. 190 показаны графики зависимостей координаты x(t), скорости υ(t) и ускорения a(t) точки, совершающей гармонические колебания. Все эти зависимости описываются гармоническими функциями одного периода (одинаковой частоты), сдвинутыми друг относительно друга на четверть периода, (которой соответствует сдвиг фазы на \(~\frac{\pi}{2}\)). Между нулями и экстремумами этих функций существуют очевидные соответствия: координата движущейся точки достигает максимального и минимального значения, когда ее скорость обращается в нуль; модуль скорости максимален, когда точка проходит через нулевую координату; модуль ускорения максимален, когда скорость равна нулю, а отклонение точки максимально.
Теперь обратим внимание, на чрезвычайно интересное и важное соотношение между ускорением точки и ее координатой[3], которое следует из сравнения функций (8) и (3):
|
|
При гармонических колебаниях ускорение точки пропорционально его координате, с отрицательным коэффициентом пропорциональности.
При изучении механического движение мы неоднократно подчеркивали, что известная зависимость ускорения тела \(~\vec a(t, \vec r, \vec \upsilon)\) от времени, координат, скорости при известных начальных условиях позволяет однозначно найти закон движения – зависимость координат от времени \(~\vec r(t)\), то есть решить основную задачу механики. Уравнение (9) является частным случаем этой задачи: ускорение зависит от координаты, причем элементарным образом, оно просто пропорционально ей. Следовательно, если на основании динамических законов нам удастся показать, что в некоторой реальной физической системе выполняется уравнение (9), то мы можем однозначно утверждать, что эта система может совершать гармонические колебания.
Мы получили это важнейшее уравнение исходя из рассмотрения закона движения (3). Теперь мы можем решить обратную задачу: если при движении материальной точки ее ускорение связано с координатой соотношением (9), то зависимость координаты от времени описывается функцией:
В этом выражении параметры A0 (амплитуда колебаний) и φ0 (начальная фаза) могут быть любыми – при любых значениях этих параметров, функция (10) удовлетворяет уравнению (9).
Заметим, что, не смотря на указанный произвол в решении уравнения (9), само уравнение уже немало говорит о возможных движениях системы: во-первых, оно указывает, что движение есть гармоническое колебание, во-вторых, однозначно указывает частоту колебаний. Коэффициент пропорциональности в этом уравнении есть квадрат круговой частоты, взятый с противоположным знаком.
Вспомним. Пусть все силы, действующие на тело постоянны, и по величине, и по направлению. В этом случае из законов динамики следует, что движение тела является равноускоренным, причем величина ускорения также определяется на основании этих же законов. Однако, для однозначного нахождения закона движение требуется задание начальных условий.
Чтобы однозначно определить закон движения при гармонических колебаниях необходимо произвольные параметры A0 и φ0 выразить через начальные условия. Итак, пусть заданы начальные условия:
Используя тригонометрическую формулу для косинуса суммы, перепишем выражение (10) в виде
в котором вместо двух произвольных параметров A0 и φ0 введены два новых параметра:
Аналогичным образом можно преобразовать выражение[4] для скорости частицы (7)
Подставим в функции (12) и (14) начальные условия (11) получим выражения
из которых следуют искомые формулы для параметров функции (12):
Таким образом, решение уравнения (9) с начальными условиями (11) имеет вид
Не составляет труда представить эту же функцию в виде (10). Так амплитуда колебаний при заданных начальных условиях определяется выражением
а начальная фаза удовлетворят условию
Подчеркнем еще одно важнейшее свойство гармонических колебаний, описываемых уравнением (9) – период и частота этих колебаний не зависят от их амплитуды. Если амплитуда колебаний определяется начальными условиями, то их частота полностью определяется коэффициентом пропорциональности между ускорением и координатой точки.
Отметим, что формально с математической точки уравнение (9) можно рассматривать в общем виде. Пусть некоторая функция X(t) удовлетворяет условию, что ее вторая производная пропорциональна самой функции (с отрицательным коэффициентом пропорциональности)
тогда эта функция изменяется по гармоническому закону \(X(t) = A \cos (\omega t + \varphi_0)\), в котором параметры A и φ0 находят из начальных условий, а круговая частота определяется самим уравнением.
17.2.1 Фазовые траектории колебательного движения.
Рассмотрим еще один наглядный способ графического представления произвольных (не только гармонических) колебаний. Пусть закон колебательного движения описывается функцией x(t), которая обязательно является периодической. По известному закону движения можно определить зависимость скорости от времени, как производную от координаты υ(t) = (x(t))′. Введем на плоскости систему декартовую систему координат, вдоль одной из осей которой будем откладывать координату точки, а вдоль другой - ее скорость. Введенная таким образом система называется фазовой плоскостью. Две функции x(t) и υ(t) в любой момент времени определяют на этой плоскости некоторую точку, а геометрическое место этих точек образует некоторую непрерывную линию, которая называется фазовой траекторией.
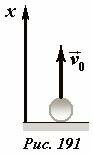
Приведем пример построения фазовой траектории. Пусть небольшой упругий шарик брошен вертикально вверх (Рис. 191) с начальной скоростью υ0. Если пренебречь сопротивлением воздуха, то скорость шарика будет изменяться со временем по закону
где g - ускорение свободного падения. Изменение координаты шарика с течением времени описывается функцией
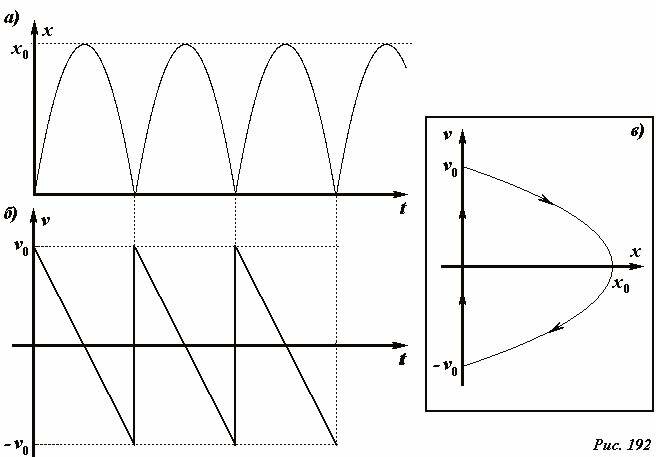
Поднявшись на максимальную высоту \(~x_0 = \frac{\upsilon^2_0}{2g}\), шарик упадет на горизонтальную поверхность и отразится от него. Если удар считать абсолютно упругим, то скорость шарика после удара примет первоначальное значение, после чего движение шарика будет повторяться. Графики зависимостей координаты и скорости шарика[5] от времени показаны на Рис. 192а, б.
Эти же функции (1), (2) определяют в параметрической форме линию на фазовой плоскости – фазовую траекторию движения шарика. Эта линия показана на Рис. 192 в. Понятно, что при периодическом движении фазовая траектория является замкнутой. На фазовой траектории принято указывать направление движения: при положительной скорости координата возрастает, а при отрицательной скорости координат убывает.
Иногда говорят, что фазовая траектория указывает зависимость скорости от координаты, но такое высказывание не всегда корректно: так одной координате может соответствовать несколько значений скорости (как в рассмотренном примере). А функциональная зависимость требует однозначного соответствия – каждому значению координаты соответствует единственное значение скорости.
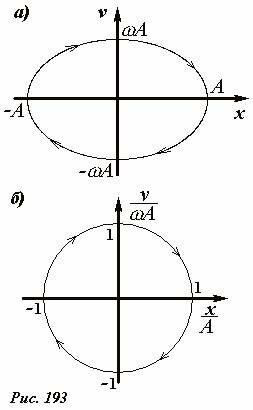
Особенно просто выглядит фазовая траектория гармонического колебания, при котором координата и скорость описываются функциями
Из этих уравнений следует, что уравнение фазовой траектории можно записать в виде
которое является уравнением эллипса[6] с полуосями A и ωA (Рис. 193 а). Еще более предпочтительным является построение фазовой траектории в относительных единицах: когда по одной оси откладывается отношение координаты к амплитуде колебаний \(~\left( \frac{x}{A} \right)\) , а на другой отношение скорости к максимальной скорости движения \(~\left( \frac{\upsilon}{\omega A} \right)\) . В этих координатах
фазовая траектория гармонического колебания является окружностью единичного радиуса (Рис. 193 б). С помощью фазовой диаграммы легко анализировать характер колебания – так отличить окружность от другой замкнутой кривой легко даже «на глаз».
17.2.2 Негармонические колебания. Разложение Фурье.
Сейчас мы покажем, что использование модели гармонических колебаний позволяет описывать и более сложные периодические движения. Еще в 1822 году французский физик и математик Жан Батист Жозеф Фурье в своей работе «Аналитическая теория теплоты» показал, что любая периодическая функция может быть представлена в виде суммы гармонических функций (то есть синусов и косинусов), при чем частоты этих функций являются кратными основной частоте. Так, если период некоторой функции x(t) равен T, то эта функция может быть представлена в виде суммы (разложения Фурье):
В общем случае эта сумма должна содержать бесконечно много слагаемых, однако в большинстве практически значимых случаев коэффициенты этого разложения достаточно быстро убывают с ростом номера k (и соответствующе ей частоты \(~\omega_k = k \frac{2 \pi}{T}\)), поэтому практически всегда с достаточной степенью точности можно ограничиться относительно небольшим числом слагаемых.
С разложением периодической функции хорошо знакомы музыканты, которые знают, что каждой ноте (основному тону), взятой на любом музыкальном инструменте соответствует целый набор кратных частот (обертонов). Набор этих колебаний с кратными частотами составляет тембр звука.
Существуют достаточно простые формулы, позволяющие находить коэффициенты разложения Фурье. Мы не собираемся в дальнейшем использовать разложение Фурье, поэтому ограничимся рядом простых примеров разложения периодических функций.
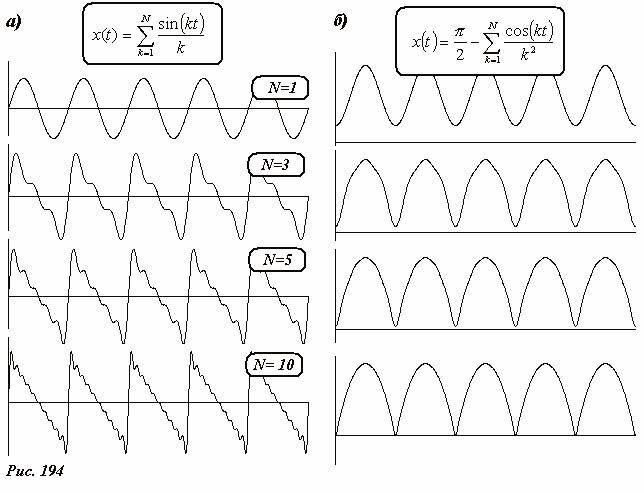
На Рис. 194 а. показаны графики функций \(~x(t) = \sum_{k=1}^N \frac{\sin (kt)}{k}\) при различных значения числа слагаемых N. Не трудно догадаться, что при больших N эти функции стремятся к рассмотренной выше зависимости скорости от времени, изображенной на Рис. 192. Даже при относительно небольшом N = 5 сходство этих функций уже вполне узнаваемо. Можно найти и разложение Фурье для зависимости координаты от времени в этом же примере, являющейся набором парабол. Эта зависимость выражается суммой \(~x(t) = \frac{\pi}{2} - \sum_{k=1}^N \frac{\cos (kt)}{k^2}\).
Графики этих функций для разного числа слагаемых изображены на Рис. 194 б.
Таким образом, с математической точки зрения прыгающий шарик вполне можно описать суммой десяти гармонических колебаний с кратными частотами.
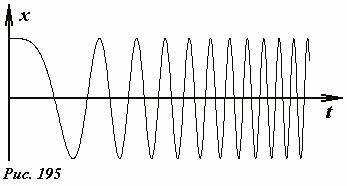
На этом мы заканчиваем рассмотрение кинематического описания колебательного движения, которое, во многом, построено на основании описания равномерного движения материальной точки по окружности. Подчеркнем, что многократное упоминание о равномерности движения не является излишним. Так как при неравномерном движении по окружности, движущаяся материальная точка, конечно, будет возвращаться в исходные положения, но не через равные промежутки времени – поэтому ее движение не будет периодическим, кроме того, скорость и ускорение также не будут изменяться периодически. Для примера, на Рис. 195 показан график зависимости координаты точки, движущейся по окружности равноускоренно. Эта функция описывается выражением \(~x = A \cos \frac{\beta t^2}{2}\). Видно, что эта функция не периодическая.
Примечания
- ↑ Подчеркнем, что не все колебания являются гармоническими, однако рассматриваемый здесь вид колебаний является простейшей моделью колебательного движения, тем не менее, достаточно часто встречающегося в действительности. Название этого вида движения связано с тем, что функции синус и косинус называются гармоническими функциями, как наиболее совершенные и изящные (по мнению некоторых математиков).
- ↑ Все эти параметры имеют явные аналоги в характеристиках движения по окружности, однако в теории колебательного движения они получили «персональные имена».
- ↑ Это соотношение настолько важно для дальнейшего изложения теории колебаний, что мы его заключили в рамку.
- ↑ Конечно, можно просто взять производную от функции (12).
- ↑ Строго говоря, процесс движения шарика не будет строго периодическим, так как скорость шарика будет изменяться вследствие сопротивления воздуха и неупругости его ударов, но этими факторами мы пренебрежем. Кроме того, удар шарика и изменение его скорости происходит не мгновенно, а в течение некоторого промежутка времени, которой пренебрежимо мало по сравнением со временем его свободного движения.
- ↑ Можно дать следующее «определение» этой хорошо знакомой линии: эллипс – «это круг, который можно вписать в квадрат со сторонами 3×4».