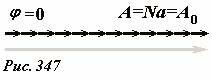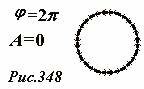Слободянюк А.И. Физика 10/19.5
§19. Волновые процессы
19.5 Дифракция волн.
19.5.1 Принцип Гюйгенса-Френеля.
В свое время мы потратили достаточно много усилий, чтобы обосновать прямолинейность распространения волн в однородной среде. Однако, отклонения от прямолинейности распространения является скорее правилом, а не исключением. Совокупность подобных явлений легко продемонстрировать с помощью поверхностных волн: волны огибают препятствия, заходя в область геометрической тени, волна, попадающая на отверстие в препятствии, порождает за ним расходящуюся волну.
Явление отклонения от прямолинейного распространения называется дифракцией волн. Иногда дифракцией называют огибание волнами препятствий[1].
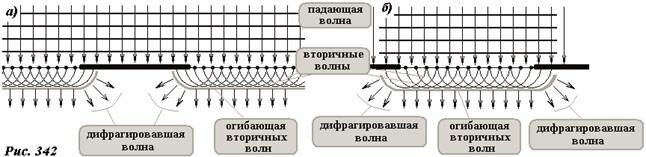
Существование дифракции волн качественно может быть обосновано принципом Гюйгенса. Пусть плоская волна падает нормально на плоское препятствие (Рис. 342а). В соответствии с принципом Гюйгенса построим семейство сферических вторичных волн. В местах, где имеется препятствие, такие волны отсутствуют, поэтому вблизи краев препятствия огибающая фронтов вторичных волн изгибается – то есть фронт результирующей волны перестает быть плоским. Следовательно, возникает отклоненная, дифрагировавшая волна, заходящая в область геометрической тени. Аналогично, можно качественно объяснить расширение волны, пошедшей через отверстие в препятствии (Рис. 342б).
Однако принцип Гюйгенса не позволяет количественно рассчитать пространственное распределение амплитуд результирующей волны. Существенный шаг в описании явления дифракции волн сделал в начале XIX века французский ученый Огюст Френель, который дополнил принцип Гюйгенса идеей интерференции. О. Френель предложил, не просто строить огибающую вторичных волн, а суммировать колебания, производимые этими волнами в каждой пространственной точке.
Дополненный этой идеей принцип получил название принципа Гюйгенса-Френеля: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, результирующая волна является результатом интерференции вторичных волн.
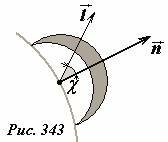
Безусловно, шаг, сделанный О. Френелем в теории волновых процессов был революционным. На основании этой основной идеи О.Френель сумел объяснить и рассчитать целый явлений, особенно, касающихся дифракции света. Однако, принцип Гюйгенса-Френеля нельзя отнести к числу фундаментальных физических законов, по своей сути он также является правилом, позволяющим рассчитывать волновую картину, но нуждающимся в своем строгом обосновании. Во времена Френеля самым существенным обоснованием этого принципа являлись следствия, результаты, полученные на его основе. Для того чтобы достичь лучшего согласия между результатами расчетов и экспериментальными данными самому О. Френелю пришлось постулировать (потому, что не мог объяснить), что амплитуда вторичной сферической волны не является одинаковой по всем направлениям, а убывает с ростом угла χ между нормалью к волновому фронту \(~\vec n\) и направлением распространения \(~\vec l\) вторичной волны. Поразительно, но О.Френель правильно «угадал» вид этой зависимости. На Рис. 343 она условно показана как уменьшение толщины контура вторичной волны. При небольших углах χ уменьшение амплитуды мало, поэтому мы ею в дальнейшем будем пренебрегать.
Обоснование рассматриваемого принципа дал в середине XIX века немецкий физик Кирхгоф. Он показал, что решение волнового уравнения может быть представлено в виде суммы слагаемых, каждое из которых можно интерпретировать как сферическую вторичную волну переменной амплитуды. Таким образом, принцип Гюйгенса-Френеля следует рассматривать как правило, вытекающее из волнового уравнения. Сами же волновые уравнения следуют из физических законов, описывающих волновые движения сред.
19.5.2 Дифракция волн на щели.
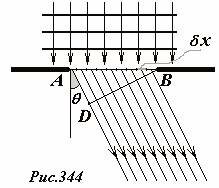
Изучение дифракции волн начнем с простого случая, который позволит, тем не менее, позволит нам оценить условия, при которых дифракция волны существенна, и при каких ею можно пренебречь. Пусть плоская монохроматическая волна падает нормально на плоскую стенку, в которой проделана щель AB шириной |AB| = b (Рис. 344). Рассчитаем амплитуды дифрагировавшей волны в произвольных точках пространства за стенкой, находящихся на расстояниях, значительно превышающих размер щели. Чтобы воспользоваться принципом Гюйгенса-Френеля, мысленно разобьем щель на малые не перекрывающиеся участки шириной δx, которые будем рассматривать как источники вторичных волн. Число таких участков равно \(~N = \frac{b}{\delta x}\). Так как каждая точка щели является источником вторичных волн, то для корректного расчета результата их интерференции, мы обязаны считать число источников бесконечно большим, то есть осуществить переход от N дискретных источников волн к одному непрерывному протяженному источнику – всем точкам щели. Для этого необходимо перейти к пределу N → ∞ , общая же ширина всех источников должна оставаться равной ширине щели b. Следовательно, размер каждого источника должен стремиться к нулю δx → 0 , соответственно и амплитуда каждой вторичной волны также должна стремиться к нулю. Разумно считать, что амплитуда вторичной волны пропорциональна размеру участка разбиения δx.
Поставленная задача аналогична расчету интерференции волн от цепочки N точечных источников, которую мы рассмотрели в разделе 19.4.2. В данном случае, мы также полагаем, что точка наблюдения находится достаточно далеко, поэтому для расчета разности фаз между колебаниями, порожденными в этой точке вторичными волнами, можно воспользоваться приближением «интерференции параллельных лучей». Иными словами, мы будем полагать, что положение точки наблюдения определятся углом θ между нормалью к волновой поверхности падающей волны и направлением на точку наблюдения – в данном случае его называют углом дифракции. Амплитуда результирующей волны от N одинаковых, колеблющихся в одной фазе источников, нами найдена ранее и равна
где a - амплитуда, колебания, создаваемого одним источником, \(~\Delta \varphi = \frac{2 \pi}{\lambda} d \sin \theta\) - разность фаз колебаний от двух соседних источников, d - расстояние между источниками, которое в рассматриваемом случае следует положить равным δx. Сейчас, для описания дифракции плоской волны нам фактически необходимо в формуле (1) перейти к пределу N → ∞ , не забывая, что при этом и разности фаз Δφ, и амплитуды a стремятся нулю. Прежде всего, заметим, что произведение φ = NΔφ имеет смысл разности фаз колебаний, создаваемых крайними источниками, поэтому оно не зависит от числа интервалов разбиения. Формально, это выражение можно преобразовать следующим образом
Как мы отмечали, амплитуда отдельной вторичной волны пропорциональна размеру участка разбиения \(~\delta x = \frac{b}{N}\), поэтому ее можно представить в виде
где A0 - коэффициент пропорциональности, физический смысл которого мы выясним чуть ниже. Наконец, воспользуемся тем, что при ξ → 0 sin ξ → ξ. С учетом этих замечаний, формулу (1) можно преобразовать к виду
где φ - разность фаз колебаний, создаваемых между крайними точками щели, которая определяется по формуле (2).
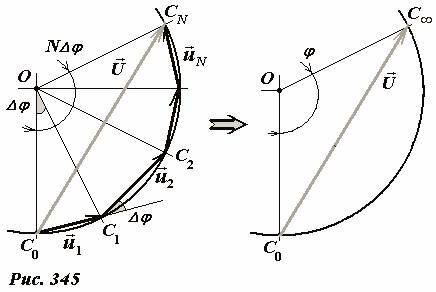
Проделанный предельный переход может быть также осуществлен и с помощью метода векторных диаграмм. Так векторная диаграмма колебаний, создаваемых N источниками построена на рис. 345 и представляет собой ломанную, состоящую из N равных по длине звеньев, наклоненных под одним и тем же углом Δφ друг к другу. При переходе к непрерывному распределению источников вторичных волн, эта ломанная стремится к дуге окружности (Рис. 345), причем угол между касательными к этой дуге, проведенными в ее крайних точках равен разности фаз колебаний, создаваемых крайними источниками вторичных волн.
Тогда длина вектора результирующего колебания может быть найдена из равнобедренного треугольника С0OС∞:
где R - радиус дуги окружности. Если пренебречь зависимостью амплитуды вторичной волны от направления ее распространения, то длины векторов, изображающих колебания отдельных вторичных волн будут постоянны при изменении угла θ ( и связанной с ним разности фаз φ). Поэтому суммарная длина ломанной в дискретном случае и длина дуги в непрерывном пределе будут оставаться неизменными. Обозначим неизменную длину дуги предельной векторной диаграммы A0, она связана с радиусом этой дуги соотношением
Теперь достаточно разделить соотношение (5) на (6), чтобы получить формулу (4). При таком подходе сразу понятен смысл величины A0 - сумма амплитуд колебаний, создаваемых всеми вторичными волнами (в том числе и при переходе к их непрерывному распределению).
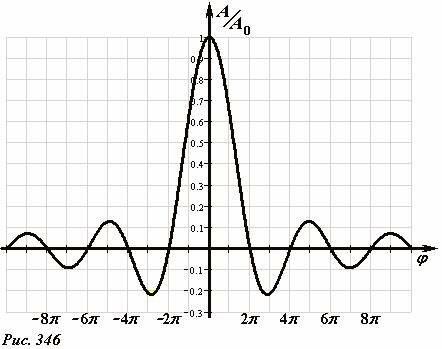
Проанализируем полученное распределение амплитуды дифрагировавшей волны (4). Полученная функция является непрерывной, ее график показан на рис. 346. Даже при φ → 0 она не имеет разрыва, так как соответствующий этой точке предел конечен (математики называют его «первым замечательным пределом»):
Заметим, что φ = 0 при угле θ = 0, поэтому введенный параметр A0 равен амплитуде волны, распространяющейся в том же направлении, что и падающая волна.
При φ = 0 дуга векторной диаграммы становится отрезком прямой (Рис. 347), понятно, что в этом случае амплитуда результирующего колебания максимальна. С ростом разности фаза амплитуда результирующего колебания изменяется, проходя через максимумы и минимумы. Абсолютное значение амплитуды в точках экстремумов монотонно уменьшается, так даже в точке первого минимума оно составляет чуть более 20% от величины центрального максимума. Анализируемая функция обращается в нуль, когда ее числитель равен нулю, то есть при
Не трудно заметить, что при этих разностях фаз векторная диаграмма замыкается в окружность (по которой следует пройти n раз). Так на рис. 348 она показана для важного случая φ = 2π.
Таким образом, можно считать, что наиболее значимым в этой функции является центральный максимум, ширина которого равна расстоянию между двумя ближайшими нулями δφ = 4π.
Обратите внимание на принципиальные отличия данной предельной функции (4) от ее «прародительницы» (1), которую мы проанализировали ранее. Функция (4) имеет только один главный максимум. Еще более существенное различие, часто приводящее к определенным недоразумениям: при интерференции волн от точечных, дискретных источников, при разности фаз колебаний между ними Δφ = 2π - наблюдается максимум. При интерференции волн, испущенных непрерывным источником, при разности фаз между колебаниями его крайних точек равным тем же φ = 2π результата сложения – нуль. Дело в том, что в первом случае мы складываем две (или несколько) синусоид максимумы и минимумы которых совпадают, а во втором складывается бесконечно много синусоид с плавным изменением сдвига фаз между ними – поэтому каждой из них имеет противоположная по фазе, в результате все они гасят друг друга.
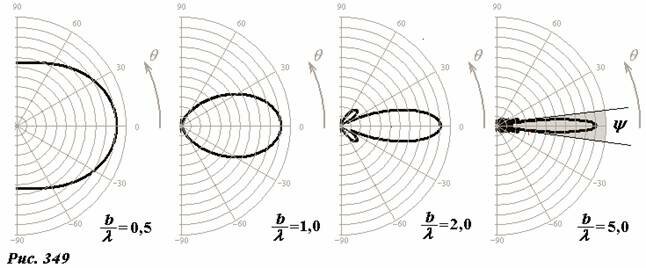
Так как разность фаз колебаний φ, создаваемых крайними точками щели, зависит от угла дифракции θ (по формуле (2)), то фактически мы получили зависимость амплитуды волны от угла дифракции. На рис. 349 представлены индикатрисы дифракции (зависимости амплитуды результирующей волны от угла дифракции, построенные в полярной системе), рассчитанные по формулам (4) и (2).
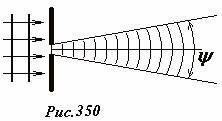
Из вида этой функции (и из графиков) видно, что угловое распределение дифрагировавшей волны полностью определяется отношением ширины щели к длине волны \(~\frac{b}{\lambda}\). Чем больше ширина щели, тем уже угловое распределение. Если ширина щели значительно превышает длину падающей волны, то после такой щели волна практически полностью распространяется в том же направлении, что и исходная падающая волна, в такой ситуации дифракцией можно пренебречь, то есть считать полностью справедливым закон прямолинейного распространения волн. Реально за такой щелью волна представляет собой слегка расходящийся поток плоской волны, поперечный размер которого примерно совпадает с размером отверстия. Волновые поверхности этого пучка вблизи отверстия, по-прежнему, плоские, а по мере удаления от него слегка искривляются (Рис. 350).
Угол расхождения этого пучка может быть оценен на основании полученного углового распределения амплитуд. Амплитуда дифрагировавшей волны обращается в нуль при угле дифракции θ0, при котором разность фаз колебаний от крайних точек щели становится равной 2π. При малых углах дифракции (когда ширина щели значительно превышает длину волны) синус угла примерно равен самому углу sin θ0 ≈ θ0, поэтому этот угол оценивается из равенства
из которого следует, что угол расходимости волнового пучка (см. рис. 250) равен
Полученный результат является универсальным – чем меньше отношение длины волны к размерам препятствия (или к размерам отверстий) тем менее существенную роль играют дифракционные явления.
Угол расходимости волнового пучка может быть оценен по формуле (10) для отверстия любой формы, так как форма отверстия несущественно влияет на коэффициент пропорциональности между углом расходимости и отношением \(~\frac{\lambda}{b}\). Так, например, для отверстия круглой формы этот коэффициент на 22% больше, чем для рассмотренной щели.
С другой стороны, если размер отверстия заметно меньше длины волны, то такое отверстие фактически может рассматриваться как источник сферической волны. В этом случае амплитуда дифрагировавшей волны слабо зависит от направления ее распространения, что подтверждает первая диаграмма на рис. 349. Фотография волн на поверхности воды, сформированных после узкой щели качественно подтверждает справедливость полученных результатов (Рис. 350). Эта же фотография может служить иллюстрацией принципа Гюйгенса, наглядно демонстрируя «реальность» вторичных волн.
Расчет дифракционной картины на основании принципа Гюйгенса-Френеля для препятствий других форм проводится аналогично – открытая часть волнового фронта разбивается на бесконечно малые участки, каждый из которых рассматривается как источник сферической вторичной волны. После чего проводится суммирование (точнее интегрирование) колебаний, создаваемой в каждой пространственной точке этими вторичными волнами. То есть с точки зрения физических законов алгоритм решения такой задачи известен. Однако практическое выполнение такого суммирования является сложной математической задачей, которая может быть решена аналитически только в некоторых простейших случаях. Кроме того, в общем случае в общем случае необходимо учитывать уменьшение амплитуды с ростом расстояния от источника, а также зависимость этой амплитуды от направления распространения вторичной волны. Поэтому для ее анализа и приближенного решения О.Френелем и его последователями разработан целый ряд оригинальных методов, с некоторыми из которых мы познакомимся при изучении дифракции света. Отметим, также, что в настоящее время для выполнения расчетов дифракционных картин широко используются численные расчеты с помощью компьютера.
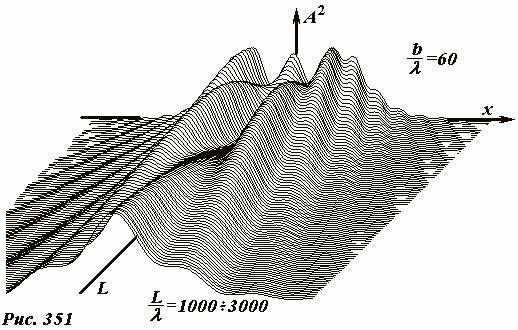
Чтобы продемонстрировать сложность (но и выполнимость) расчета дифракционной картины на рис. 351 показана зависимость квадрата амплитуды волны дифрагировавшей на щели в зависимости от расстояния до оси системы и от расстояния до щели L. При расчет проведен на основании принципа Гюйгенса-Френеля с учетом зависимости амплитуд вторичных волн от расстояния и от направления их распространения. Как видите, при изменении расстояния от щели распределение амплитуд качественно изменяется число максимумов и минимумов, они меняются местами, и только на больших расстояниях формируется распределение аналогичное рассмотренному нами в приближении «интерференции параллельных лучей».
Примечания
- ↑ Трудно дать строгое и однозначное определение дифракции – так, например, под данное в тексте определение попадает и преломление волны на границе раздела двух сред. Трудно провести четкую границу между этими и другими волновыми явлениями: то же преломление света в линзе может быть описано как в рамках геометрической оптики, так и на основании волновых дифракционных представлений. Кстати, сам термин дифракция происходит от латинского difractus – разломанный.