Слободянюк А.И. Физика 10/19.6

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.6 Описание волновых явлений с помощью волновых уравнений, или «Почему от квадратного кирпича волны круглые?»

При изучении различных волновых явлений мы неоднократно подчеркивали, что использованные нами методы являются приближенными и не всегда строго обоснованными. Более строгий подход к теоретическому изучению этих явлений основывается на выводе волновых уравнений и их решении. Такой подход изобилует многочисленными математическими сложностями. Тем не менее, в данном разделе мы попытаемся продемонстрировать его принципиальную осуществимость.

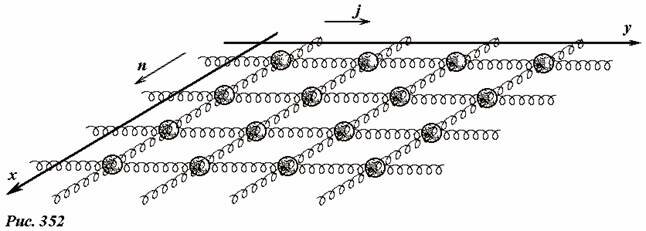
В качестве модельной системы мы используем квадратную решетку, состоящую из одинаковых массивных шариков, соединенных невесомыми упругими пружинками – двумерным аналогом упругой цепочки, с которой мы начали изучение волновых процессов (Рис. 352). Направим оси декартовой системы координат вдоль граней решетки. Пронумеруем шарики двумя индексами: n (n = 0,±1,±2...) вдоль оси Ox; j ( j = 0,1,±2...) вдоль оси Oy. Для наглядности рассмотрим поперечные колебания решетки. В этом случае ее движение описывается набором функций u_{n, j}(t) - зависимостью отклонения шарика с индексами (n, j) от времени. На основании второго закона Ньютона можно показать, что ускорения шариков зависят от его смещения и смещений его соседей в соответствии с уравнением

\(~a_{n,j} = \frac{c^2}{l^2}((u_{n-1,j} - u_{n,j}) + (u_{n+1,j} - u_{n,j}) + (u_{n,j-1} - u_{n,j}) + (u_{n,j+1} - u_{n,j}))\) , (1)

где c - скорость распространения волны, зависящая от массы шариков, длины l и силы натяжения пружинок. Каждое слагаемое в правой части этого уравнения является вертикальной проекцией силы упругости пружинок, действующих на выбранный шарик.

Мы уже показывали, что при переходе к непрерывному распределению масс и сил упругости (то есть при переходе от дискретной сетки к непрерывной мембране) эта система уравнений переходит к волновому уравнению для функции трех переменных u(x,y,t), описывающей возмущение мембраны

\(~\frac{\partial^2 u}{\partial t^2} = c^2 \left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right)\) . (2)

Отметим, что это уравнение является следствием физических законов: в рассматриваемом случае – законов Ньютона и Гука; для звуковых волн такое же уравнение следует из газовых законов; для электромагнитных волн – следует из уравнений Максвелла.

Фактически система уравнений (1) является аналогом волнового уравнения. Для однозначного решения этой системы (или волнового уравнения (2)) необходимо задать начальные условия (значения начальных смещений u⁽⁰⁾_n,j и скоростей всех шариков υ⁽⁰⁾_n,j), а если сетка ограничена, то и граничные условия – в простейшем случае можно считать, что все шарики на границе сетки закреплены.

Для численного решения системы уравнений непрерывно текущее время удобно также сделать «дискретным» - рассматривать значения смещений шариков в некоторые моменты времени, разделенные малыми временным промежутками τ. Также пронумеруем эти моменты времени индексами i (i = 0,1,2,3...). Таким образом, вместо поиска непрерывной функции от трех переменных u(x,y,t) ставится задача определения ее значений в дискретных точках u_n,j,i. Ускорение шарика в момент времени \(t_i = i \tau\) приближенно можно заменить отношением изменения скорости шарика к промежутку времени τ. Скорость же шарика приближенно равна отношению изменения его смещения к такому же промежутку времени, то есть

\(~a_{n,j,i} \approx \frac{\frac{u_{n,j,i+1} - u_{n,j,i}}{\tau} - \frac{u_{n,j,i} - u_{n,j,i-1}}{\tau}}{\tau} = \frac{u_{n,j,i+1} + u_{n,j,i-1} - 2u_{n,j,i}}{\tau^2}\) . (3)

Подстановка этого выражения в систему уравнений (1) приводит к системе алгебраических уравнений для определений смещений шариков в дискретные моменты времени

\(~\begin{matrix} u_{n,j,i+1} + u_{n,j,i-1} - 2u_{n,j,i} = \frac{c^2 \tau^2}{l^2}((u_{n-1,j} - u_{n,j}) + (u_{n+1,j} - u_{n,j}) + (u_{n,j-1} - u_{n,j}) + (u_{n,j+1} - u_{n,j})) = \\ = \frac{c^2 \tau^2}{l^2}(u_{n-1,j} + u_{n+1,j} + u_{n,j-1} + u_{n,j+1} - 4 u_{n,j}) \end{matrix}\) . (4)

Уравнение (4) позволяет выразить смещение шарика в момент времени (i + 1), через смещения его и его соседей в предыдущие моменты времени:

\(~u_{n,j,i+1} = -u_{n,j,i-1} + 2u_{n,j,i} + \frac{c^2 \tau^2}{l^2}(u_{n-1,j} + u_{n+1,j} + u_{n,j-1} + u_{n,j+1} - 4 u_{n,j})\) . (5)

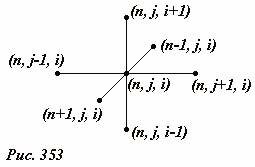
Графически схема уравнений (5) показана на рис. 353. Таким образом, если известны все значения смещений в два последовательных момента времени (i − 1) и i, то выражение (5) позволят найти значения смещения всех шариков в следующий момент времени (i + 1). Для того, чтобы «запустить» последовательное решение системы (5) следует воспользоваться начальными условиями: так значения смещений в начальный момент времени задается начальными смещениями

\(~u_{n,j,0} = u^{(0)}_{n,j}\) , (6)

а значения смещений в следующий момент времени τ может быть приближенно рассчитаны с помощью значений начальных скоростей

\(~u_{n,j,1} \approx u^{(0)}_{n,j} + \tau \upsilon^{(0)}_{n,j}\) . (7)

Итак, соотношения (5)-(7) позволяют последовательно рассчитать движение рассматриваемой системы. Отметим также, что безразмерный параметр \(~\frac{c \tau}{l}\) в уравнениях (4)-(5) имеет явный физический смысл: отношение расстояния, проходимого волной за выбранный промежуток времени сτ, к периоду решетки l. Для корректности полученных результатов этот параметр должен быть значительно меньше единицы. Уменьшение этого параметра приводит к уменьшению погрешности данного приближенного алгоритма.

Конечно, такие расчеты весьма громоздки и реально осуществимы только с помощью компьютера. Кроме того, реальные схемы численных решение волновых уравнений носят более сложный характер – проведение таких расчетов составляет предмет отдельного обширного раздела прикладной математики. Тем не менее, и рассмотренная здесь схема имеет право на реализацию.

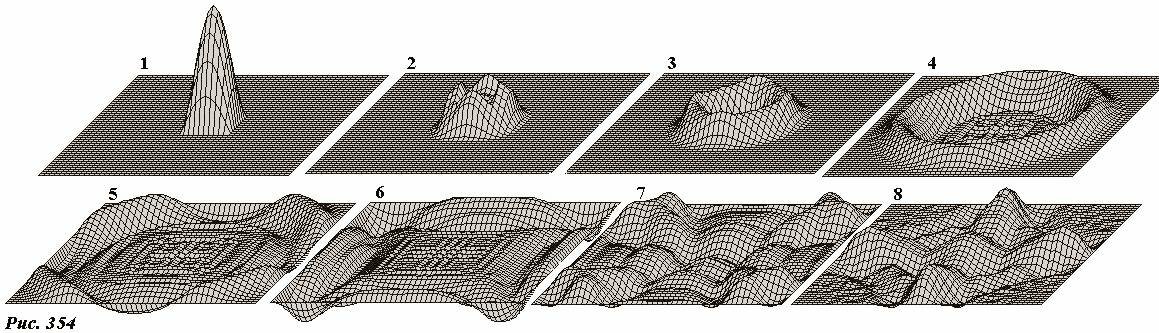
Для примера, на рис. 354 приведены результаты расчетов колебаний квадратной пластинки – показаны профили пластинки в различные моменты времени. При расчетах безразмерный параметр \(~\frac{c \tau}{l}\) принимался равным 0,01 - его дальнейшее уменьшение не приводило к видимым изменениям в получаемых «картинках».

Каждая сторона пластинки была разбита на 51 отрезок (всего 51× 51 = 2601 квадратных участков). В качестве начальных условий была задана «горбообразная» функция, отличная от нуля в пределах небольшого квадрата в центре пластинки, значения всех начальных скоростей равны нулю: эти условия близки к тем, как образуется волна от брошенного в воду квадратного бруска.

Физические процессы, проиллюстрированные этими рисунками, понятны и изучались нами:

1 - начальное распределение возмущений;

2 - расплывание начального возмущения;

3 - формирование круговой волны (плоские волны от каждой грани по мере удаления превращаются в круговые – подобное явление мы рассматривали при изучении дифракции);

4 - сформировавшаяся круговая волна, распространяющаяся от источника при этом ее форма остается круговой (подобный эффект мы назвали прямолинейным распространением);

5 - волна достигла границ пластинки и начинает отражаться от них (закрепленная сторона пластинки является границей раздела, от которой происходит отражение волны);

6- первичная волна достигла угловых точек, начинает формироваться сложная стоячая волна как результат интерференции падающих и отраженных волн;

7,8 - сформировалась сложная комбинированная стоячая волна, являющаяся суперпозицией большого числа собственных мод колебаний пластинки.

Таким образом, приведенный пример показывает, что все рассмотренные ранее явления могут быть описаны с единой точки зрения, поэтому провести резкие грани и дать их точные определения затруднительно.

Примечания

Следующая страница