Слободянюк А.И. Физика 10/19.7

Содержание книги

Предыдующая страница

§19. Волновые процессы

19.7 Энергия волны, перенос энергии.

Любая волна является движением некоторой среды. Поэтому среда, возмущенная проходящими волнами, обладает дополнительной энергией, которую мы будем называть энергий волны. Подчеркнем, что на самом деле речь идет об энергии движущихся и взаимодействующих между собой частиц среды, подобно тому, как следует строго говорить о кинетической энергии движущегося тела (а не энергии движения); о потенциальной энергии взаимодействующих тел (а не энергии взаимодействия).

Волновое движение своеобразно: все частицы среды колеблются около своих положений равновесия, в среднем не перемещаясь, а волна распространяется на произвольно большие расстояния, вместе с ней передается энергия. Возможность передачи энергии волной представляет большой интерес.

Мы рассмотрим перенос энергии в упругой волне, распространяющейся по упругой цепочке, которая уже неоднократно использовалась нами в качестве простой модели среды, в которой могут распространяться волны. Как и ранее, многие результаты, полученные в рамках этой модели, оказываются «универсальными», применимыми для всех типов волнового движения.

19.7.1 Кинематика упругой волны – длинноволновое приближение.

Итак, пусть по бесконечной цепочки, состоящей из небольших шариков, массы m, соединенных невесомыми пружинками жесткости γ длиной l, распространяется продольная упругая волна. Закон движения шарика (его смещение от положения равновесия) номер n описывается функцией

\(~u_n(t) = A \cos (\omega t - n \Delta \varphi)\) . (1)

При этом его скорость и ускорение изменяются со временем по законам

\(~\upsilon_n(t) = -A \omega \sin (\omega t - n \Delta \varphi)\) , (2) \(~a_n(t) = -A \omega^2 \cos (\omega t - n \Delta \varphi)\) . (3)

Вместо набора функций u_n(t), описывающих движение каждого шарика, можно использовать функцию двух переменных: времени и координаты шарика

\(~u(x,t) = A \cos \left(\omega t - \frac{\Delta \varphi}{l} x \right)\) , (4)

которая появляется при переходе от описания движения дискретной цепочки шариков к колебаниям непрерывной струны. В этом случае номер шарика может быть выражен через его координату \(~n \to \frac{x}{l}\). При такой записи явно видно, что величина \(~\frac{\Delta \varphi}{l} = k\) представляет собой волновое число, поэтому скорость распространения волны равна

\(~c = \frac{\omega}{k} = \frac{\omega l}{\Delta \varphi}\) . (5)

При изучении такой волны мы показали, что разность фаз между колебаниями двух соседних шариков подчиняется соотношению

\(~\cos \Delta \varphi = 1 - \frac{\omega^2}{\omega^2_0}\) , (6)

где \(~\omega_0 = \sqrt{\frac{2 \gamma}{m}}\) - собственная частота колебаний отдельного шарика.

Для упрощения математических выкладок, мы будем описывать свойства волны в «длинноволновом приближении», когда частота волны значительно меньше собственной частотой колебаний отдельного шарика \(~\omega << \omega_0 = \sqrt{\frac{2 \gamma}{m}}\), а длина волны значительно превышает расстояния между центрами шариков. В этом практически важном приближении сдвиг фаз между колебаниями соседних шариков является малой величиной Δφ << 1, поэтому для косинуса этой величины применима приближенная формула

\(~\cos \Delta \varphi \approx 1 - \frac{1}{2} (\Delta \varphi)^2\) .

Подставляя это выражение в формулу (6), получим уравнение

\(~\cos \Delta \varphi \approx 1 - \frac{1}{2} (\Delta \varphi)^2 = 1 - \frac{\omega^2}{\omega^2_0}\) , (7)

из которого получаем простое выражение для сдвига фаз:

\(~\Delta \varphi \approx \sqrt{2} \frac{\omega}{\omega_0} = \omega \sqrt{\frac{m}{\gamma}}\) . (8)

Скорость распространения волны в этом случае оказывается равной

\(~c = \frac{\omega}{k} = l \sqrt{\frac{\gamma}{m}}\) (9)

и не зависящей от частоты волны. Запишем также несколько равносильных выражений для сдвига фаз между колебаниями соседних шариков

\(~\Delta \varphi = \frac{\omega l}{c} = 2 \pi \frac{l}{Tc} = 2 \pi \frac{l}{\lambda}\) . (10)

Эти выражения в явном виде выражают сдвиг фаз через отношения: времени распространения волны между соседними шариками \(~\tau = \frac{l}{c}\) к периоду колебаний \(~T = \frac{2 \pi}{\omega}\) волны; расстояния между шариками к длине волны λ = cT. Эти отношения являются малыми величинами одного порядка. В дальнейших выкладках можно использовать приближенные формулы, оставляя в них только те члены, которые имеет первый порядок малости по этим отношениям. Так, например, тригонометрические функции с указанной точностью приближенно выражаются как cos Δφ ≈ 1, sin Δφ ≈ Δφ.

Формулы (10) становятся очевидными и банальными, если вспомнить, что за время периода колебаний их фаза изменяется на 2π, а разность фаз колебаний точек, расположенных на расстоянии длины волны, также равна 2π.

Выразим теперь закон движения (n + 1)-го шарика через характеристики колебаний его предыдущего n-го соседа, для чего используем тригонометрическую формулу для косинуса суммы:

\(~\begin{matrix} u_{n+1}(t) = A \cos (\omega t - (n+1) \Delta \varphi) = A \cos ((\omega t - n \Delta \varphi) - \Delta \varphi) = \\ = A \cos (\omega t - n \Delta \varphi) \cos \Delta \varphi + A \sin (\omega t - n \Delta \varphi) \sin \Delta \varphi \approx \\ \approx A \cos (\omega t - n \Delta \varphi) - \frac{\Delta \varphi}{\omega} (-A \omega \sin (\omega t - n \Delta \varphi)) = u_n(t) - \frac{l}{c} \upsilon_n(t) \end{matrix}\) . (11)

Полученная формула очень интересна: отношение \(~\tau = \frac{l}{c}\) равно времени распространения волны от одного шарика до следующего за ним. Выражение (11) показывает, что смещение (n + 1)-го шарика в данный момент времени t равно смещению предыдущего в предшествующий момент времени \(~t - \frac{l}{c}\).

Сравним два выражения

\(~\begin{matrix} u_{n+1}(t) = u_n(t) - \upsilon_n(t) \tau \\ u_n(t + \tau) = u_n(t) + \upsilon_n(t) \tau \end{matrix}\) ,

которые явно демонстрируют общее свойство распространяющихся волн: сдвиг в пространстве на величину l равносилен сдвигу во времени на величину \(~\tau = -\frac{l}{c}\). Это свойство справедливо для всех распространяющихся волн. Любая волна описывается функцией U(x,t)= F(x − ct), поэтому для нее справедливо

\(~U(x + l,t) = F(x + l - ct) = F \left(x - c \left( t - \frac{l}{c} \right) \right) = U \left(x, t - \frac{l}{c} \right)\) .

Соотношение, аналогичное (11), можно получить и для скоростей соседних шариков

\(~\begin{matrix} \upsilon_{n+1}(t) = -A \omega \sin (\omega t - (n+1) \Delta \varphi) = -A \omega \sin ((\omega t - n \Delta \varphi) - \Delta \varphi) = \\ = -A \omega \sin (\omega t - n \Delta \varphi) \cos \Delta \varphi - A \omega \cos (\omega t - n \Delta \varphi) \sin \Delta \varphi \approx \\ \approx -A \omega \sin (\omega t - n \Delta \varphi) + \frac{\Delta \varphi}{\omega} A \omega^2 \sin (\omega t - n \Delta \varphi) = \upsilon_n(t) - \frac{l}{c} a_n(t) \end{matrix}\) . (11)

19.7.2 Средняя плотность энергии волны.

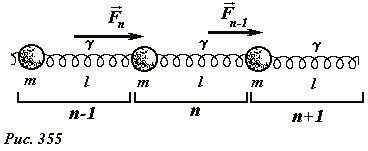
Теперь с помощью полученных кинематических законов рассмотрим энергетические характеристики волны, распространяющейся по цепочке. Мысленно разобьем цепочку на одинаковые элементарные ячейки, включающие шарик и следующую за ним пружину (Рис. 355).

Кинетическая энергия одной ячейки совпадает с кинетической энергией движущегося шарика, ее зависимость от времени выражается формулой

\(~W_{kin, n} = \frac{m \upsilon^2_n}{2} = \frac{m A^2 \omega^2}{2} \sin^2 (\omega t - n \Delta \varphi)\) . (13)

Во многих случаях основной интерес представляет среднее значение кинетической энергии, которое легко определить из выражения (13)

\(~<W_{kin, n}> = <\frac{m A^2 \omega^2}{2} \sin^2 (\omega t - n \Delta \varphi)> = \frac{m A^2 \omega^2}{4}\) , (14)

где учтено, что среднее значение квадрата синуса равно \(~\frac{1}{2}\). Причем, особо отметим, что в данном случае усреднение можно понимать двояко: как усреднение по промежутку времени, значительно превышающему период колебаний; либо как усреднение по участку цепочки, длина которого значительно превышает длину распространяющейся волны. В первом случае мы, как бы, следим за движением одного шарика в течение некоторого промежутка времени; во втором – рассчитываем среднюю энергию большого числа шариков в заданный момент времени. В случае гармонической волны такие усреднения временное и пространственное приводят к одному результату.

При переходе к непрерывному пределу от цепочки к непрерывной струне удобной характеристикой является средняя плотность энергии – энергия, приходящаяся на единицу длины струны. Для расчета этой характеристики следует среднюю энергию одной ячейки (14) разделить на ее длину

\(~<w_{kin, n}> = \frac{<W_{kin, n}>}{l} = \frac{\rho A^2 \omega^2}{4}\) , (15)

где обозначено \(~\rho = \frac{m}{l}\) - средняя плотность цепочки, масса единицы длины.

Проведем расчет потенциальной энергии выделенной ячейки, то есть энергию пружинки, которая пропорциональна квадрату ее деформации

\(~U_n = \frac{\gamma (u_{n+1} - u_n)^2}{2}\) . (16)

Из этой формулы следует, что потенциальная энергия ячейки зависит от разности смещений двух соседних шариков. Эту разность удобно выразить с помощью формулы (11)

\(~U_n = \frac{\gamma}{2} \left( -\frac{l}{c} \upsilon_n \right)^2 = \frac{\gamma l^2}{2 c^2} \upsilon^2_n = \frac{m \upsilon^2_n}{2} = W_{kin}\) . (17)

Полученный результат является неожиданным: в любой момент времени потенциальная энергия ячейки равна ее кинетической энергии. Этот же вывод справедлив и для средней плотности потенциальной энергии

\(~<w_{pot, n}> = \frac{<U_n>}{l} = \frac{\gamma l^2}{2 c^2} <\upsilon^2_n> = \frac{\gamma l}{4} \frac{A^2 \omega^2}{c^2} = \frac{\rho A^2 \omega^2}{4}\) . (18)

Вспомните: при колебаниях маятника (как пружинного, так и математического) потенциальная энергия максимальна, когда кинетическая равна нулю, и наоборот - колебания этих двух видов энергии происходят в противофазе. В упругой волне эти колебания синфазны. Это принципиально различное поведение качественно может быть объяснено следующим образом: для пружинного маятника потенциальная энергия определяется его собственным смещением от положения равновесия, а для упругой волны эта энергия зависит от разности смещений двух соседей. Можно также указать, что для непрерывной среды ее кинетическая энергия пропорциональна производной от смещения по координате \(~\upsilon = \frac{\partial u}{\partial t}\), а ее относительная деформация равна производной по координате \(~\varepsilon = \frac{\partial u}{\partial x}\). В случае незатухающей волны эти производные изменяются со временем по одному закону, следовательно, одинаково изменяются кинетическая и потенциальная энергии.

Суммарная средняя плотность энергии упругой волны определяется по формуле

\(~<w> = <w_{kin, n}> + <w_{pot, n}> = \frac{\rho A^2 \omega^2}{2}\) , (19)

она пропорциональна квадрату амплитуды волны и квадрату ее частоты.

Приведем еще одно выражение для плотности потенциальной энергии. Выразим потенциальную энергию пружинки через ее относительную деформацию \(~\varepsilon_n = \frac{u_(n+1) - u_n}{l}\):

\(~U_n = \frac{\gamma (u_{n+1} - u_n)^2}{2} = \frac{\gamma l^2 \varepsilon^2_n}{2}\) .

Теперь средняя потенциальная энергия оказывается равной

\(~w_{pot, n} = \frac{U_n}{l} = \frac{\gamma l^2 \varepsilon^2_n}{2} = \frac{E \varepsilon^2}{2}\) ,

где E = γl - введенный ранее модуль Юнга среды. Сравните полученное выражение с формулами для средних плотностей энергии электрического и магнитного полей!

19.7.3 Поток энергии в упругой волне.

При распространении волны по цепочке происходит постоянная передача энергии от одной ячейки к другой. Для описания этого переноса удобно ввести специальную характеристику S – поток энергии, равны количеству энергии, передаваемой по цепочки в единицу времени. В нашей модели эта величина может быть рассчитана работа, совершаемая в единицу времени (то есть мощность) пружинкой ячейки номер (n − 1) над шариком n-ой ячейки, поэтому

\(~S_{n-1} = P_{n-1} = F_{n-1} \upsilon_n = \gamma (u_{n-1} - u_n) \upsilon_n\) . (20)

Выразим поток энергии через характеристики движения (n − 1)-ой ячейки, для чего используем формулы (11)-(12):

\(~S_{n-1} = \gamma (u_{n-1} - u_n) \upsilon_n = \gamma \left(u_{n-1} - \left(u_{n-1} - \frac{l}{c} \upsilon_{n-1} \right) \right) \left(\upsilon_{n-1} - \frac{l}{c} a_{n-1} \right) = \gamma \frac{l}{c} \upsilon_{n-1} \left(\upsilon_{n-1} - \frac{l}{c} a_{n-1} \right)\) .

Все расчеты мы проводим в длинноволновом приближении, оставляя только малые величины первого порядка, поэтому в полученном выражении следует опустить последнее слагаемое пропорциональное квадрату времени распространения волны между соседними ячейками \(~\left( \frac{l}{c} \right)^2\). В этом случае получаем формулу

\(~S_{n-1} = \gamma \frac{l}{c} \upsilon_{n-1} \left(\upsilon_{n-1} - \frac{l}{c} a_{n-1} \right) = \gamma \frac{l}{c} \upsilon^2_{n-1} = c \frac{\gamma l}{c^2} \upsilon^2_{n-1} = c \frac{m \upsilon^2_{n-1}}{l} = c w_{n-1}\) , (21)

которая разумна и понятна: поток энергии равен произведению плотности энергии на скорость распространения волны. Следует также подчеркнуть, что рассчитанный поток энергии является положительной величиной, то есть действительно энергия постоянно передается в одном направлении. Иными словами, энергия «привязана» к волне и распространяется вместе с ней. Такое же вывод справедлив и для среднего (во времени) потока энергии, который равен произведению средней плотности энергии на скорость волны

\(~ = c <w>\) . (22)</center>

Понятно, что средний поток энергии постоянен вдоль всей цепочки.

Наконец, рассчитаем разность потоков энергии, поступающей в выделенную ячейку и отдаваемую ей следующему соседу за малый промежуток времени

<center>\(~(S_{n-1} - S_n) \Delta t = (c \rho \upsilon^2_{n-1} - c \rho \upsilon^2_n)\Delta t\) .</center>

Для преобразования в очередной раз используем выражение (12) и пренебрегаем слагаемыми второго порядка малости

<center>\(~c \rho \left( \left( \upsilon_n + \frac{l}{c} a_n \right)^2 - \upsilon^2_n \right) \Delta t = c \rho \left( 2 \upsilon_n \frac{l}{c} a_n \right) \Delta t = 2 l \rho \upsilon_n (a_n \Delta t)\) .</center>

Последний шаг преобразований мы выполняли не один раз \(~\upsilon_n (a_n \Delta t) = \upsilon_n \Delta \upsilon_n = \Delta \left( \frac{\upsilon^2_n}{2} \right)\). В итоге получаем

<center>\(~(S_{n-1} - S_n) \Delta t = 2 l \Delta \left( \frac{\rho \upsilon^2_n}{2} \right) = \Delta W_n\) ,</center>

где W_n - полная энергия ячейки (сумма равных между собой кинетической и потенциальной энергий). В итоге получаем искомый результат

<center>\(~(S_{n-1} - S_n) = \frac{\Delta W_n}{\Delta t}\) (23)</center>

- разность потоков энергии поступающей и вытекающей из ячейки равна скорости изменения ее полной энергии. Очевидно и ожидаемо – закон сохранения энергия справедлив и в данном случае!

Полученные результаты могут быть обобщены на случай упругой волны, распространяющейся в трехмерном пространстве. Для такой волны можно ввести объемные плотности кинетической, потенциальной и полной энергии \(~w = \frac{\Delta W}{\Delta V}\) - отношение соответствующей энергии ΔW, заключенной в объеме ΔV к величине этого объема (с последующим переходом ΔV → 0).

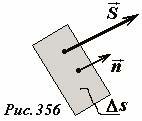
Вместо потока энергии по линейной цепочки необходимо использовать понятие вектора плотности потока энергии \(~\vec S\) : количество энергии, перетекающей в единицу времени через площадку единичной площади, ориентированную перпендикулярно направлению распространения волны (Рис. 356):

<center>\(~\vec S = \frac{\Delta W}{\Delta t \Delta s} \vec n\) . (24)</center>

Для этих «точечных» энергетических характеристик справедливы следующие утверждения:

- средние объемные плотности кинетической и потенциальной энергии равны между собой и пропорциональны квадрату амплитуды волны;

- колебания плотностей кинетической и потенциальной энергии происходят в одной фазе;

- плотность потока энергии равна произведению объемной плотности энергии волны на скорость ее распространения;

- поток вектора плотности потока энергии через любую замкнутую поверхность равен скорости изменения энергии внутри данной поверхности.

В дальнейшем мы убедимся, что аналогичные утверждения справедливы и для электромагнитных волн – то ли природе не хватает разнообразия, то ли нам, людям, воображения.

Примечания