Слободянюк А.И. Физика 10/3.2

Содержание книги

Предыдующая страница

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.2 Движение материальной точки по произвольной кривой

Если угловая скорость не является постоянной, то имеет смысл ввести понятие углового ускорения, которое мы обозначим греческой буквой ε («эпсилон»).

Угловым ускорением называется отношение изменения угловой скорости к промежутку времени, в течение которого это изменение произошло, при промежутке времени, стремящемся к нулю.

\(~\varepsilon = \frac{\Delta \omega}{\Delta t}\) , при Δt → 0 . (1)

Используя связь между линейной и угловой скоростями, эту формулу можно переписать в виде

\(~\varepsilon = \frac{\Delta \omega}{\Delta t} = \frac{1}{R}\frac{\Delta \upsilon}{\Delta t}\) .

Заметим, что в данном выражении в числителе стоит изменение модуля скорости (а не вектора скорости!). Полное же ускорение - отношение изменения вектора скорости к промежутку времени, таким образом, оказывается состоящим из двух частей - одна из которых описывает изменение направления вектора скорости (это ускорение является центростремительным или нормальным ), а вторая - изменение модуля скорости (это ускорение называется касательным или тангенциальным).

Если направление вектора скорости не изменяется, то вектор ускорения направлен вдоль той же прямой, что и скорость, поэтому следует считать, что вектор тангенциального ускорения совпадает с направлением вектора скорости, если скорость возрастает и противоположен ему, если величина скорости убывает.

При движении материальной точки по произвольной кривой, малый участок траектории можно приближенно заменить небольшой дугой окружности. Для этого следует воспользоваться следующим способом построения такой окружности, который аналогичен построению касательной прямой. Напомним, что касательную можно считать предельным положением секущей прямой.

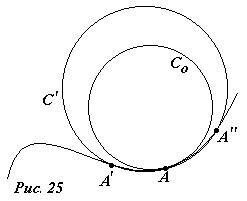
Возьмем слева и справа от точки A две точки A’, A’’ , лежащие на заданной линии (рис. 25). Проведем через эти три точки окружность секущую C’ , (если три точки лежат на одной прямой, то мы будем считать эту прямую окружностью очень большого радиуса). После этого начнем мысленно приближать точки A’, A’’ к точке A, соответственно изменяя секущую окружность. При стремлении точек A’, A’’ к точке A секущая окружность будет стремиться к предельному положению C₀. Эта предельная окружность называется соприкасающейся в точке A, ее радиус называется радиусом кривизны линии в данной точке, а центр центром кривизны.

Таким образом, движение по произвольной кривой на малом участке можно рассматривать как движение по соприкасающейся окружности.

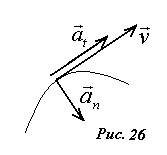
Вектор скорости \(~\vec \upsilon\) частицы всегда направлен по касательной к линии траектории движения, а вектор ускорения можно разложить на две составляющие (см. рис. 26) - одна из них, тангенциальное ускорение \(~\vec a_t\) , описывает изменение модуля скорости и направлено по касательной к траектории, а другая, нормальное ускорение \(~\vec a_n\), описывает изменение направления вектора скорости и направлено перпендикулярно касательной (по нормали) к центру кривизны траектории (в сторону ее вогнутости).

Модули этих компонент ускорений рассчитываются по формулам

\(~a_t = \frac{\Delta \upsilon}{\Delta t} = \varepsilon R ; a_n = \frac{\upsilon^2}{R} = \omega^2 R\) , (2)

где R - радиус кривизны траектории в данной точке.

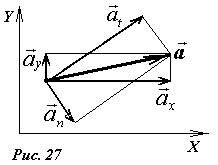
Сумма векторов ускорений \(~\vec a_t\) и \(~\vec a_n\) является вектором полного ускорения \(~\vec a\). Конечно, вектор полного ускорения можно представить в виде суммы проекций \(~\vec a_x\) и \(~\vec a_y\) на произвольно выбранные оси координат (рис. 27). Но разложение вектора на нормальную и тангенциальную составляющие имеет два существенных преимущества: первое, обе компоненты \(~\vec a_t\) и \(~\vec a_n\) имеют явные физический смысл; второе, такое разложение «привязывается» не к произвольно выбранной системе координат, а непосредственно к траектории движения и вектору скорости.

Примечания

Следующая страница