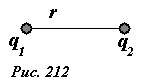Слободянюк А.И. Физика 10/9.13
§9. Электрическое поле и его свойства
9.13 Энергия электрического поля. Плотность энергии.
Вернемся к обсуждению вопроса об энергии взаимодействия электрических зарядов. Ранее мы показали, что потенциальная энергия электростатического взаимодействия двух точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга (рис. 212), рассчитывается по формуле
Придадим этой формуле несколько иной вид
здесь \(~\varphi_1 = \frac{1}{4 \pi \varepsilon_0} \frac{q_2}{r}\) - потенциал поля, создаваемого вторым зарядом, в точке, где находится первый заряд. Аналогично можно записать
где \(~\varphi_2 = \frac{1}{4 \pi \varepsilon_0} \frac{q_1}{r}\) - потенциал поля, создаваемого первым зарядом, в точке, где находится второй заряд. Теперь, перепишем выражение (1), в симметричной форме, легко допускающей обобщение
В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и появляется в формуле множитель 1/2.
Если система состоит из нескольких зарядов q1, q2, …, qN , то полная энергия их взаимодействия есть сумма энергий взаимодействий всех пар зарядов. Используя симметричное выражение (2), суммирование по парам зарядов (двойную сумму), можно заменить на суммирование по самим зарядам, то есть записать
В этой формуле φk - потенциал поля в точке, где находится заряд qk, причем поля, создаваемого всеми зарядами, кроме самого заряда qk (как говорят, исключая самовоздействие заряда на самого себя).
Использование понятия энергии взаимодействия требует чрезвычайной точности и внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны, предоставляет определенную свободу, а, с другой, требует четкого понимания о какой именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Если же требуется рассчитать работу поля при изменении положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от нулевого уровня потенциала.
Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим примеры расчета энергии электростатического взаимодействия.
Три точечных заряда.
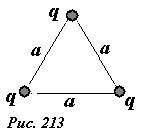
Пусть три одинаковых точечных заряда, величины которых равны между собой q1 = q2 = q3 = q, расположены в вершинах правильного треугольника со стороной a (рис.213). Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен
В соответствии с формулой (3) энергия взаимодействия зарядов равна
Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное расстояние друг от друга.
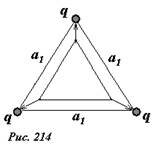
Если заряды сместятся, так что окажутся в вершинах правильного треугольника со стороной a1 , то их энергия окажется равной
При таком смещении работа электрического поля будет равна уменьшению энергии системы
Обратите внимание, при \(~a_1 \to \infty\) эта работа становится в точности равной начальной энергии U0.
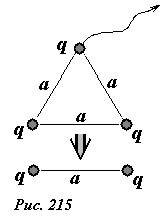
Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся (рис. 215), то энергия системы станет равной
При этом поле совершит работу
Если теперь удалить еще один заряд, то энергия системы станет равной нулю, при этом поле совершит работу A2 = U1. В итоге начальная энергия полностью расходуется на совершение полной работы U0 = A1 + A2 .
Задание для самостоятельной работы.
- Проанализируйте изменение энергии и совершенные работы в рассмотренной системе, если один из зарядов отрицательный.
Энергия взаимодействия двух равномерно заряженных параллельных пластин.
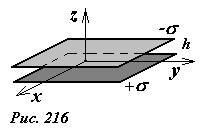
Найдем энергию взаимодействия двух равных по модулю зарядов противоположного знака, равномерно распределенными по двум параллельным пластинам. Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой -σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин, площадь каждой пластины обозначим S. Краевыми эффектами пренебрежем.
Для расчета энергии взаимодействия воспользуемся формулой U = qφ’, где φ’ - потенциал поля создаваемого всеми зарядами, кроме заряда q.
Напряженность поля между пластинами была вычислена нами ранее, она равна
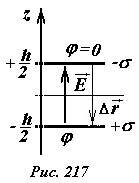
Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен
Здесь \(~\Delta \vec r\) - вектор перемещения от отрицательной пластины к положительной. Данная формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.
Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами \(~E' = \frac{E}{2} = \frac{\sigma}{2 \varepsilon_0}\) , поэтому искомый потенциал будет равен \(~\varphi' = E'h = \frac{\sigma h}{2 \varepsilon_0}\) . Таким образом, энергия взаимодействия зарядов оказывается равной
здесь σS - заряд положительно заряженной пластины.
Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.
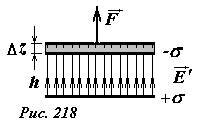
Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения \(~F = q E' = (\sigma S) \frac{\sigma}{2 \varepsilon_0} = \frac{\sigma^2}{2 \varepsilon_0} S\) , причем эта сила не зависит от расстояния между пластинами. Для того, чтобы раздвинуть пластины на расстояние h, необходимо приложить внешнюю силу, равную по модулю силе электрического притяжения (рис. 218). При этом эта сила совершит работу (равную увеличению энергии системы)
Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε0E, выразим энергию взаимодействия через напряженность поля
В процессе разнесения пластин создается электрическое поле во все большем объеме между пластинами, поэтому можно утверждать, что совершенная работа увеличивает энергию электрического поля, или работа расходуется на создание поля. Так при смещении пластины на расстояние Δz, объем занятый полем увеличивается на SΔz, если расстояние между пластинами увеличилось от нуля до некоторого значения h, то поле создается в объеме Sh. Таким образом, найденная энергия взаимодействия зарядов (7) есть энергия электрического поля - энергия «размазанная» по той области пространства, где создано поле. Косвенным подтверждением сделанного заключения, является тот факт, что энергия взаимодействия пропорциональна объему части пространства V = Sh, занятого полем и выражается через характеристику поля (его напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже благодаря своему существованию обладает энергией. В качестве энергетической характеристики поля следует рассматривать энергию, содержащуюся в единице объема, то есть объемную плотность энергии\[~w = \frac{W}{V}\] . Из выражения (8) следует, что объемная плотность энергии электрического поля определяется формулой
Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю
Энергия поля равномерно заряженной сферы.
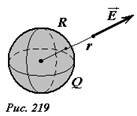
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна
в частности непосредственно у поверхности сферы напряженность поля равна
Обратим внимание, что произведение \(~S = 4 \pi R^2\) есть площадь сферы, поэтому отношение \(~\frac{Q}{4 \pi \varepsilon_0} = \sigma\) является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе \(~E_0 = \frac{\sigma}{\varepsilon_0}\). Потенциал поверхности сферы также был вычислен нами ранее
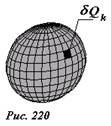
Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны \(~\delta Q_k = \frac{Q}{N}\) (k = 1,2…N). Рассмотрим один из этих малых зарядов. В точке его расположения потенциал поля, создаваемого всеми остальными (N-1) зарядами равен \(~\varphi_k = \frac{(N-1) \delta Q}{4 \pi \varepsilon_0 R}\). С использованием симметричной формулы \(~U = \frac{1}{2} \sum_{k} {q_k \varphi_k}\) , выражение для энергии взаимодействия приобретает вид
данная сумма содержит N одинаковых слагаемых, поэтому равна
Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе \(~N \to \infty\) слагаемое \(~\frac{1}{N}\) исчезает, поэтому окончательное выражение для энергии взаимодействия зарядов сферы имеет вид
Заметим, что полученное выражение имеет вид \(~U = \frac{1}{2} Q \varphi_0\). Если сразу заявить, что уменьшение заряда на малую величину \(~\delta Q\) пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.
Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда \(~\delta Q_k = \frac{Q}{N}\) (k = 1,2…N), которые будем переносить на сферу из «бесконечности». Если сфера не заряжена, то перенесение первой «порции» заряда не требует совершения никакой работы. После того как сфера приобрела некоторый электрический заряд, перенесение следующей порции заряда требует совершения работы по преодолению сил отталкивания со стороны зарядов сферы. Если на сферу перенесено (k-1) порций заряда, то ее потенциал равен \(~\varphi_{(k-1)} = \frac{(k-1) \delta Q}{4 \pi \varepsilon_0 R}\) . Поэтому для того, что бы перенести на сферу следующую порцию заряда необходимо совершить работу
Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.
Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии
Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов (\(~N \to \infty\)) мы опять приходим к формуле (14).
В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.
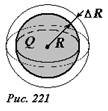
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя \(~\Delta V = 4 \pi R^2 \Delta R\) . Пренебрегая изменением напряженности поля в пределах тонкого слоя, энергию, заключенную в нем запишем в виде
где w - плотность энергии поля. С другой стороны эта энергия равна изменению энергии взаимодействия зарядов при увеличении радиуса сферы
На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности \(~Q = 4 \pi \varepsilon_0 R^2 E\) :
Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой \(~w = \frac{\varepsilon_0 E^2}{2}\).