Слободянюк А.И. Физика 10/9.14

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.14 Энергия поля и энергия взаимодействия зарядов.

Рассмотрим еще раз взаимодействие двух точечных зарядов q₁ и q₂, находящихся на расстоянии друг от друга. Мы показали, что энергия их взаимодействия рассчитывается по формуле

\(~U(r) = \frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r}\) . (1)

С другой стороны, мы показали, что электрическое поле обладает энергией, объемная плотность которой определяется формулой

\(~w = \frac{\varepsilon_0^2 E}{2}\) . (2)

Для того чтобы рассчитать полную энергию электрического поля W, напряженность которого изменяется от точки к точке, необходимо разбить пространство, где существует поле на малые объемы ΔV_k, в каждом из которых вычислить плотность энергии поля w_k (если изменяется напряженность поля, то изменяется и его плотность энергии), после чего просуммировать энергию по всему пространству, где существует поле

\(~W = \sum_{k} {w_k \Delta V_k}\) . (3)

Выполнить такое суммирование не всегда просто, но, тем не менее, такая операция вполне выполнима. В данном случае нас интересуют не математические проблемы, связанные с вычислением подобных сумм, а физический смысл получаемых результатов.

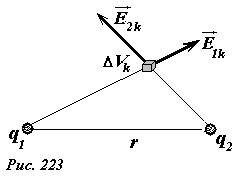
Применим формулы (2)-(3) к расчету энергии поля, создаваемого двумя точечными зарядами. По принципу суперпозиции напряженность электрического поля в произвольной точке, окруженной объемом ΔV_k равна сумме напряженностей полей, создаваемых каждым зарядом в отдельности (рис. 223)

\(~\vec E_k = \vec E_{1k} + \vec E_{2k}\) .

Полную энергию поля запишем в виде

\(~W = \sum_{k} {w_k \Delta V_k} = \sum_{k} {\frac{\varepsilon_0}{2} (\vec E_{1k} + \vec E_{2k})^2 \Delta V_k} = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k}^2 \Delta V_k} + \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{2k}^2 \Delta V_k} + 2 \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k} \cdot \vec E_{2k} \Delta V_k}\) . (4)

Прежде всего, обратим внимание, что для энергии поля принцип суперпозиции не выполняется – энергия системы зарядов не равна сумме энергий зарядов, взятых по отдельности. Математическим выражением нарушения принципа суперпозиции является нелинейная зависимость энергии от напряженности поля – плотность энергии пропорциональна квадрату напряженности. Если напряженность поля увеличится в два раза, то плотность энергии увеличивается в четыре раза! Кстати, аналогичное заключение можно сделать и для полученной ранее энергии заряженной сферы – энергия пропорциональная квадрату заряда.

Первое слагаемое в формуле (4)

\(~W_1 = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k}^2 \Delta V_k}\)

полностью определяется зарядом q₁ и не зависит от наличия второго заряда – это слагаемое описывает энергию поля, создаваемого этим зарядом. Аналогично, второе слагаемое

\(~W_2 = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{2k}^2 \Delta V_k}\)

описывает энергию поля, создаваемого зарядом q₂. Наконец третье слагаемое

\(~W_{vz} = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k} \cdot \vec E_{2k} \Delta V_k}\) ,

зависит от величин зарядов и от взаимного расположения. Аккуратное вычисление этой суммы приводит к результату

\(~W_{vz} = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k} \cdot \vec E_{2k} \Delta V_k} = \frac{q_1 q_2}{4 \pi \varepsilon_0 r} = U\) .

Таким образом, это слагаемое определяет энергию взаимодействия зарядов, которая является частью энергии электрического поля.

Если сами заряды не изменяются, то первые два слагаемых в энергии поля (4) не изменяются при изменении взаимного расположения зарядов, поэтому их можно не учитывать. Вспомните – протекание всех физических процессов определяется изменением энергии, поэтому постоянная, не изменяющаяся часть энергии для описания этих процессов не существенна.

Мы показали, что энергия заряженной сферы обратно пропорциональна ее радиусу. Точечный заряд можно рассматривать как заряженную сферу бесконечно малого радиуса. При стремлении радиуса сферы к нулю (при сохранении ее заряда) энергия поля стремится к бесконечности - энергия поля точечного заряда бесконечно велика. Конечно, можно утверждать, что точечный заряд является математической абстракцией. Однако, до настоящего времени не известно никаких экспериментальных данных о том, что электрон имеет конечные размеры, поэтому должен рассматриваться как реально существующий точечный заряд. Эта серьезная проблема современной физики еще ждет своего разрешения.

Аналогичным образом можно рассмотреть энергию поля, создаваемого несколькими точечными зарядами q₁, q₂, q₃ … Энергия поля, рассчитанная с помощью принципа суперпозиции и формулы (3), представляется в виде

\(~\begin{matrix} W = \sum_{k} {w_k \Delta V_k} = \sum_{k} {\frac{\varepsilon_0}{2} (\vec E_{1k} + \vec E_{2k} + \vec E_{3k} + \ldots)^2 \Delta V_k} = \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k}^2 \Delta V_k} + \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{2k}^2 \Delta V_k} + \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{3k}^2 \Delta V_k} + \ldots + \\ + 2 \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k} \cdot \vec E_{2k} \Delta V_k} + 2 \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{1k} \cdot \vec E_{3k} \Delta V_k} + \ldots + 2 \sum_{k} {\frac{\varepsilon_0}{2} \vec E_{2k} \cdot \vec E_{3k} \Delta V_k} + \ldots = \\ = W_1 + W_2 + W_3 + \ldots + U_{12} + U_{13} + \ldots + U_{23} + \ldots \end{matrix}\) . (5)

То есть энергия этого поля является суммой энергий полей отдельных зарядов и энергий всех парных взаимодействий.

Интересно отметить, что если бы плотность энергии зависела от напряженности не квадратично, а по более сложному закону, то в полной энергии появились бы слагаемые, учитывающие тройные и другие взаимодействия.

Таким образом, формулы (2)- (3) описывают полную энергию электрического поля, а формула (1) только ее часть – энергию взаимодействия, изменяющуюся при измени взаимного расположения зарядов.

Наконец, обсудим еще один парадокс, связанный с расчетами энергии электрического поля. При расчете энергии взаимодействия зарядов, распределенных по поверхности сферы, нами получен следующий результат

\(~U = \frac{Q^2}{8 \pi \varepsilon_0 R}\) .

Расчет полной энергии электрического поля равномерно заряженной сферы приводит к тому же результату! Таким образом, кажется, что собственная энергия зарядов «исчезает». Покажем, что это противоречие возникло при разбиении заряда на бесконечно малые части. Если исходный заряд разбит на N частей, величиной \(~\delta Q = \frac{Q}{N}\) каждый, то энергия взаимодействия эти зарядов между собой пропорциональна квадрату заряда \(~(\delta Q)^2\) и числу взаимодействующих пар \(~\frac{1}{2} N(N-1)\). Таким образом \(~U \propto (\delta Q)^2 N (N-1) = \left ( \frac{Q}{N} \right )^2 N (N-1)\) , а при \(~N \to \infty \ U \propto Q^2\), то есть энергия взаимодействия не зависит от числа частей, на который мы мысленно разбиваем исходный заряд. Собственная энергия зарядов пропорциональна квадрату заряда \(~(\delta Q)^2\) и их числу N, поэтому при \(~N \to \infty\) собственная энергия стремится к нулю\[~W_{sob} \propto N (\delta Q)^2 = N \left ( \frac{Q}{N} \right )^2 = \frac{Q^2}{N} \to 0\] . Строго говоря, предельный переход \(~\delta Q \to 0\) физически некорректен, так электрический заряд дискретен – существует минимальный электрический заряд. Тем не менее, учитывая малость элементарного заряда, наши расчеты обеспечивают достаточную точность.

Кстати, при расчете энергии заряженной сферы мы также пренебрегли слагаемым пропорциональным \(~\frac{1}{N}\). Для того, чтобы учесть дискретность заряда (то есть, заряжать сферу по одному электрону), следует положить \(~N = \frac{Q}{e}\) , где e - элементарный заряд.

Примечания

Следующая страница