Слободянюк А.И. Физика 10/9.2
§9. Электрическое поле и его свойства
9.2. Напряженность электрического поля точечного заряда.
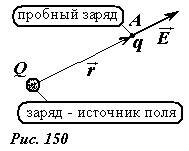
Рассмотрим электрическое поле, создаваемое одним точечным зарядом. Чтобы подчеркнуть, что этот заряд мы рассматриваем как источник поля, обозначим его величину прописной буквой Q (рис. 150).
Возьмем произвольную пространственную точку A. Для определения напряженности электрического поля, поместим в эту точку пробный заряд q. Согласно закону Ш. Кулона, сила, действующая на пробный заряд равна
где \(~vec r\) — вектор, проведенный от заряда источника Q, к точке A, в которой рассчитывается поле (точку наблюдения). Тогда, по определению, напряженность поля в этой точке равна
и, заметьте, не зависит от величины пробного заряда. Формула (1), определяет напряженность электрического поля, создаваемого точечным зарядом.
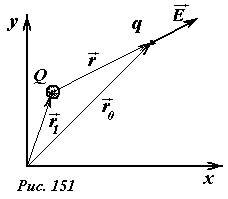
Фактически формула (1) определяет вектор напряженности в зависимости от 6 координат: трех координат заряда и трех координат точки наблюдения. Введем декартовую систему координат (рис. 151), пусть в этой положение заряда определяется радиус-вектором \(~\vec r_1\) (или координатами (x1, y1, z1)), а положение точки наблюдения — радиус-вектором \(~\vec r_0\) (или координатами (x0, y0, z0)).
Тогда вектор \(~\vec r\) , соединяющий заряд и точку наблюдения, фигурирующий в формуле (1), равен \(~\vec r = \vec r_0 - \vec r_1\) . Следовательно, напряженность поля в точке наблюдения определяется формулой
Перепишем эту формулу в координатной форме. Длина вектора \(~\vec r = \vec r_0 - \vec r_1\) равна \(~|\vec r_0 - \vec r_1| = \sqrt{(x_0 - x_1)^2 + (y_0 - y_1)^2 + (z_0 - z_1)^2}\) , а его проекция на ось X - \(~(\vec r_0 - \vec r_1)_x = x_0 - x_1\). Следовательно, проекция вектора напряженности на ось X определяется по формуле
Две аналогичных формулы надо выписать и для оставшихся компонент вектора напряженности. Оцените очередной раз прелесть векторной записи (2) — во-первых, короче; во-вторых, не зависит от выбора системы координат, хотя конкретные численные расчеты, все равно необходимо проводить в координатной форме.