Слободянюк А.И. Физика 10/9.3

Содержание книги

Предыдующая страница

§9. Электрическое поле и его свойства

9.3. Принцип суперпозиции для напряженности электрического поля

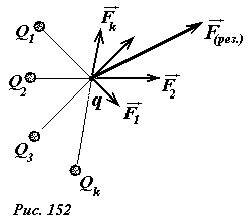
Для расчета поля, создаваемого нескольким точечными зарядами, следует воспользоваться принципом суперпозиции. Пусть электростатическое поле создается системой зарядов (рис. 152) Q₁, Q₂, …, Q_N, расположенных в точках, положение которых задается радиус-векторами \(~\vec r_1, \vec r_2, \ldots, \vec r_N\) . Для определения напряженности в некоторой точке с радиус-вектором \(~\vec r_0\) , поместим в нее пробный заряд q.

По принципу суперпозиции для электростатических сил, результирующая сила, действующая на пробный заряд равна сумме сил, действующих со стороны каждого заряда в отдельности

\(~\vec F_{rez} = \frac{Q_1 q}{4\pi \varepsilon_0} \frac{\vec r_0 - \vec r_1}{|\vec r_0 - \vec r_1|^3} + \frac{Q_2 q}{4\pi \varepsilon_0} \frac{\vec r_0 - \vec r_2}{|\vec r_0 - \vec r_2|^3} + \ldots + \frac{Q_N q}{4\pi \varepsilon_0} \frac{\vec r_0 - \vec r_N}{|\vec r_0 - \vec r_N|^3} = \sum_{k=1}^{N} {\frac{Q_k q}{4\pi \varepsilon_0} \frac{\vec r_0 - \vec r_k}{|\vec r_0 - \vec r_k|^3}} \).

Для вычисления напряженности поля, эту силы необходимо разделить на величину пробного заряда. Тем самым, мы доказали принцип суперпозиции для напряженности электрического поля: напряженность поля, создаваемого системой зарядов, равна сумме напряженностей полей, создаваемых каждым зарядом в отдельности:

\(~\vec E = \vec E_1 + \vec E_2 + \ldots + \vec E_N = \sum_{k=1}^{N} {\vec E_k} = \sum_{k=1}^{N} {\frac{Q_k}{4\pi \varepsilon_0} \frac{\vec r_0 - \vec r_k}{|\vec r_0 - \vec r_k|^3}} \).

Если заряды распределены внутри некоторого тела непрерывно (заданы объемной плотностью зарядов), то для вычисления напряженности поля необходимо разбить тело на малые части, каждую из которых можно рассматривать как точечный заряд, после чего можно воспользоваться формулой (1).

Таким образом, закон Ш. Кулона и принцип суперпозиции позволяет рассчитать напряженность поля, создаваемого произвольной (но известной) системы зарядов. Правда, провести такие расчеты не легко, но это уже проблемы математики, а не физики.

Следующая страница