Kvant. Движение точки

А так ли хорошо знаете вы, как движется точка? // Квант. — 1989. — № 8. — C.40-41.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

...нельзя наблюдать и определить движения тела,
имеющего конечную величину, не определив сначала,
какое движение имеет каждая его маленькая частичка или точка.
Л. Эйлер

Замечательную возможность изучать самые разнообразные, в том числе и очень сложные, движения предоставляет сведение их к простейшему — движению точки вдоль линии. Но и такое, на первый взгляд, нехитрое движение требует для своего описания введения целого ряда понятий. В этом выпуске «Калейдоскопа» мы будем «работать» с несколькими из них — траекторией, координатой, путем и перемещением. За каждым понятием — долгая история, связанная со становлением законов, которым подчиняются движения тел на Земле и в космосе.

Вопросы и задачи

1. Столкнутся ли два шара, если известно, что траектории их центров пересекаются?
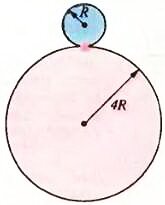
2. Круг радиусом R катится по кругу радиусом 4R. Сколько оборотов совершит малый круг по возвращении в первоначальное положение?

   

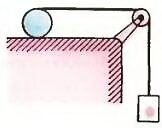
3. Нерастяжимая нить намотана на цилиндр, а другим концом привязана к грузу. Какой путь пройдет груз, когда катящийся без скольжения цилиндр, длина окружности которого равна l, сделает один оборот?

   

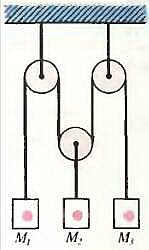
4. К нерастяжимой нити, перекинутой через блоки, привязаны грузы, как показано на рисунке. Найдите направление и модуль вектора перемещения груза M₂, если груз M₁ переместился на 5 см вверх, а груз M₃ — на 3 см вниз.

   

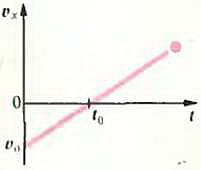
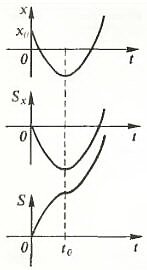
5. Тело движется прямолинейно, выйдя из точки с координатой x₀, причем проекция его скорости на ось X меняется так, как показано на графике. Как будут выглядеть для этого тела графики зависимости координаты х, проекции S_x перемещения и пути от времени?

   

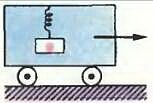
6. Какова (относительно Земли) траектория колеблющегося на пружинке грузика, помещенного в равномерно движущийся вагон?

   

7. По какой траектории движется частица в бегущей продольной волне?
8. Мальчик бросает мячи из вагона в сторону, противоположную движению поезда. Как будут двигаться мячи по отношению а) к вагону? б) к полотну дороги?
9. По какой траектории станет двигаться заряженная частица, влетевшая в однородное электрическое поле под углом к силовым линиям?
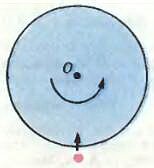
10. Существуют ли такие точки движущегося вагона, которые перемещаются не вперед, а назад? Каковы траектории этих точек?

    

11. Мелок пускают по диаметру круга. За время, пока круг делает половину оборота, мелок относительно Земли может пройти путь, равный диаметру круга. Какой след оставит мелок на круге? Трение пренебрежимо мало.

    

12. Осколки снаряда, взорвавшегося на вершине башни, разлетелись с одинаковой начальной скоростью υ₀. Как будут располагаться в пространстве осколки после взрыва? По какой траектории движется каждый осколок?

    

Микроопыт

Подвесьте тяжелый грузик (гирьку, металлический шарик) на длинной нити и отведите его на небольшой угол из положения равновесия. Отпустите грузик а) без начальной скорости; б) со скоростью, направленной перпендикулярно вертикальной плоскости, проходящей через точку подвеса. По каким траекториям начнет двигаться грузик?

Любопытно, что…

...современное понимание трехмерности физического пространства появилось, по-видимому, в XVII веке, когда Декарт изобрел прямоугольную систему координат. В древности понятие размерности пространства не применялось, так как отсутствовало понятие координат.

1. 

...только на полюсах Земли тела падают строго по вертикали. Во всех остальных точках планеты траектория свободно падающего тела отклоняется к востоку за счет так называемой силы Кориолиса, возникающей во вращающихся системах.

1. 

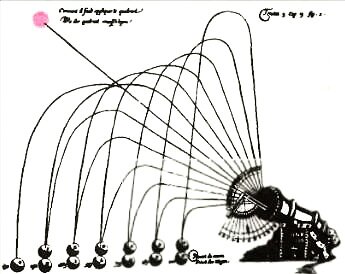
...со времен Аристотеля считалось, что траектории летательных снарядов состоят из прямолинейных отрезков и сопрягающей их дуги. И лишь Галилею удалось установить, что траекторией тела, брошенного под углом к горизонту в безвоздушном пространстве, является парабола. А итальянец Тарталья (1500—1557), хотя и не знал законов, управляющих движением снарядов, пришел к выводу, что наибольшей дальности стрельбы можно достичь, если наклонить орудие к горизонту под углом 45°.

1. 

Что читать в «Кванте» о движении точки

1. «Траектория, путь, перемещение» — 1984, № 9, с. 19;
2. «Как построить траекторию?» — 1987, № 7, с. 26;
3. «Легко ли описывать движение?» — 1987, № 9, с. 38;
4. «Основная задача кинематики» — 1988, № 9, с. 58.

Ответы

1. Однозначного ответа нет, если неизвестны размеры шаров и время их прихода к точке пересечения траекторий.
2. Пять.
3. 2l.
4. Вектор перемещения направлен вниз, его модуль равен 1 см.
5. См. рис.

   

6. Синусоида или косинусоида.
7. По отрезку прямой, лежащему на линии, совпадающей с направлением распространения волны.
8. По параболе.
9. а) По параболам; б) если скорость мяча относительно вагона равна по модулю скорости поезда относительно земли, то по вертикали; в остальных случаях — по параболам.
10. Такие точки есть на реборде колеса. Траектория одной из этих точек изображена на рис. Она называется циклоидой.

    

11. См. рис.

    

12. Осколки окажутся на поверхности раздувающейся со скоростью υ₀ сферы, центр которой опускается с ускорением g. При этом каждый осколок движется по своей параболе.

Микроопыт

а) по дуге окружности, лежащей в вертикальной плоскости;

б) по горизонтальной окружности (конический маятник).