Kvant. Магниты, заряды, планеты
Стасенко А.Л. Магниты, заряды, планеты //Квант. — 1996. — № 3. — С. 40-42.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
...физика начинает замечать, что мыслить мир — это не только его регистрировать,
но и придавать ему форму единства, которой он был бы лишен, если бы не был мыслим.
Пьер Тейяр де Шарден. Феномен человека
Что может быть проще, чем прямой провод с постоянным током I? Каждый школьник знает, что вокруг него возникает магнитное поле с кольцевыми соосными линиями вектора магнитной индукции \(~\vec B\), которые сравнительно просто можно сделать видимыми (визуализировать) при помощи классических магнитных опилок, насыпанных на лист картона, перпендикулярный к проводу. Тут, казалось бы, не о чем и говорить.
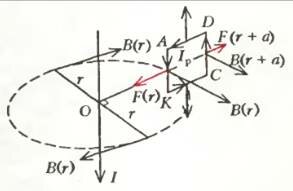
Но представим себе, что в это магнитное поле мы поместили квадратную проводящую рамку площадью а х а, в которой течет ток Ip (рис.1). Пусть две стороны рамки параллельны току, а размеры рамки много меньше расстояния r до провода, т.е. a << r. Поскольку магнитное поле, согласно выбранной геометрии, перпендикулярно всем сторонам рамки, на каждую сторону будет действовать сила Ампера, пропорциональная индукции В магнитного поля, порожденного током I, длине стороны рамки а и текущему в ней току Ip. Рассмотрим эти силы.
На сторону рамки АК, находящуюся на расстоянии r от провода, действует сила, направленная в сторону провода и равная \(~F(r) = I_p a B(r)\) (предполагается, что читатель при помощи правил буравчика и правой руки уже сообразил, куда направлены векторы \(~\vec B\), \(~\vec Ia\) и \(~\vec F\)). На сторону CD, в которой ток, естественно, противоположен по направлению току в АК, действует и противоположно направленная сила, равная \(~F(r + a) = I_p a B(r + a)\). Эта сила отличается от F(r), поскольку индукция магнитного поля зависит от расстояния до провода с током I. (Причем есть серьезное подозрение, что В уменьшается с ростом r.) А вот силы, действующие на стороны рамки AD и КС, в точности компенсируют друг друга (предполагается, что рамка не деформируется под действием этих «распирающих» сил). Значит, результирующая сила, действующая на рамку с током Ip, перпендикулярна проводу с током I и равна алгебраической сумме двух сил, действующих на стороны АК и CD:
Здесь через ΔВ обозначено приращение индукции поля В на расстоянии a << r.
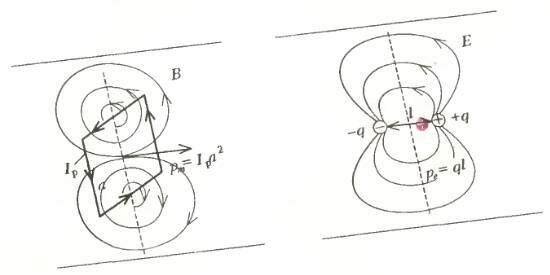
Что же мы получили? Что маленькая рамка с током Ip, лежащая в одной плоскости с прямым проводом с током I, притягивается к этому проводу с силой, пропорциональной току в рамке, ее площади и «скорости» изменения модуля индукции магнитного поля с расстоянием от прямолинейного провода (\(~\frac{\Delta B}{a}\)). Но взрослые физики не говорят так много слов. Потому что они заранее ввели некоторые определения. Так, произведение Ipa2 они назвали магнитным моментом тока \(~\vec p_m\). И не случайно, потому что линии вектора магнитной индукции \(~\vec B\) от маленькой рамки с током очень похожи на линии вектора напряженности \(~\vec E\) электростатического поля, порожденного электрическим диполем \(~\vec p_e\), конечно, на больших расстояниях (в смысле r >> а), что мы уже и предполагали с самого начала. На рисунке 2 качественно изображены картины линий векторов \(~\vec B\) и \(~\vec E\) в меридиональной плоскости. А отношение \(~\frac{\Delta B}{a} = \frac{\Delta B}{\Delta r}\) физики назвали градиентом модуля магнитного поля. Теперь вы можете гораздо короче выразить словами мысль, записанную в соотношении (1), но дело не в словах.
Дело в том, что рамка может быть любой формы (круглая, треугольная...). И вообще это может быть не рамка, а маленький магнитик (например, стрелка компаса для Дюймовочки). И внешнее магнитное поле \(~\vec B\) может быть порождено не прямым током, а каким-то другим способом. Но в любом случае сила, действующая на магнитик, помещенный во внешнее неоднородное магнитное поле, будет пропорциональна магнитному моменту тока и градиенту индукции магнитного поля. Именно эта сила, например, втягивает правильно ориентированный магнитик в соленоид с током и препятствует попыткам вынуть его оттуда.
Однако вернемся к прямому току. Интуитивно ясно, что индукция его магнитного поля как-то убывает с расстоянием. А как именно — об этом говорит один из законов Максвелла: если умножить значение индукции В(r) на длину окружности 2πr, то это произведение будет пропорционально току I, породившему магнитное поле:
Здесь введен еще коэффициент пропорциональности μ0, чтобы все было в порядке с размерностями в обеих частях равенства (в единицах СИ). Не будем обращать внимание на этот коэффициент — не в нем сейчас дело, — хотя потом, когда вы станете большими, вы вспомните и поймете, что это одна из фундаментальных констант. Сейчас же важно другое. Можно сказать, что мы записали некий закон сохранения: как бы далеко мы ни удалились от прямого (бесконечного) провода, произведение \(~B(r) \cdot 2\pi r\) остается постоянным (тут можно упомянуть, что физики называют это произведение циркуляцией магнитного поля вдоль окружности). Итак, индукция магнитного поля, порожденного прямым бесконечным током, обратно пропорциональна расстоянию от него:
Тогда как же записать отношение \(~\frac{\Delta B}{\Delta r}\) ? Кто знает, что такое производная, сразу продифференцирует полученную зависимость по радиусу и напишет
А кто не знает производную, может записать приращение обратного радиуса подробнее:
(в последнем выражении справа мы пренебрегли в знаменателе величиной Δr, считая ее малой по сравнению с самим r — ведь с самого начала мы считали, что а = Δr < r).
Пусть теперь наша маленькая рамка с током (или магнитик) имеет массу m и в некоторый момент времени движется со скоростью \(~\vec \upsilon_0\) перпендикулярно прямому току I, находясь при этом на расстоянии r0 от него. А кругом вакуум. Как она будет двигаться далее?
Мы знаем уже, что на нее действует притягивающая сила, обратно пропорциональная квадрату расстояния до провода. Где еще встречаются подобные силы? Да всюду. Согласно закону всемирного тяготения Ньютона, любые две материальные точки притягиваются друг к другу с силой, обратно пропорциональной квадрату расстояния между ними:
(Конечно, закон Ньютона описывает силу, действующую между двумя притягивающимися точками, как бы они ни были расположены в пространстве. В случае же тока и магнитика сила взаимодействия всегда лежит в плоскости, перпендикулярной току.) А согласно закону Кулона, два заряда противоположных знаков тоже притягиваются друг к другу с силой, обратно пропорциональной расстоянию между ними:
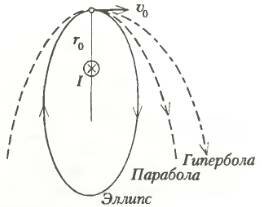
Значит, наша задача уже решена: рамка с током или магнитик будут двигаться вокруг прямого провода с током, как все тела в окрестности Солнца (рис.3) — либо по эллипсам, как планеты (если скорость υ0 не очень велика), либо по параболе или гиперболе, как залетная комета (если υ0 достаточно велика).
Таким образом, обсуждаемый процесс мы можем свести к рассмотрению процесса совсем другой физической природы (в данном случае — к решению задачи Кеплера), основываясь лишь на одинаковости уравнений, описывающих эти процессы. Поиски физических аналогий — очень увлекательное и практически полезное занятие.
Не пора ли воскликнуть: как, однако, мир един!
Но, как всегда, после первых спазмов радости, связанных с интересной находкой, нужно оглядеться — не забыто ли чего? Ну конечно, забыто.
Во-первых, успевает ли плоскость рамки с током в каждой точке своей траектории разворачиваться строго перпендикулярно линиям магнитной индукции? (Почему вообще возникает такой поворот, можно разобраться подробнее с помощью следующей заметки «Из глубин Вселенной».) Ведь рамка обладает массой и размерами (это — не точка!), значит, нужно учитывать свойство инертности при попытке повернуть рамку вокруг оси.
Во-вторых, если со временем изменяется расстояние от центра рамки до провода, изменяется и поток магнитной индукции через плоскость рамки. А это, как известно, должно бы вызвать в самой рамке ЭДС индукции, которая может изменить ток, что приведет к появлению ЭДС самоиндукции,..., тока самоиндукции, стремящегося противодействовать изменению магнитного потока от провода.
В третьих, это последнее обстоятельство должно также стремиться изменить и ток в проводе (явление взаимной индукции).
В четвертых...
Но лучше остановиться и сказать, что развитая нами теория верна при условии, если всеми этими эффектами можно пренебречь.